
科目: 來源: 題型:
【題目】設數列![]() 的通項公式為
的通項公式為![]() (
(![]() ,
, ![]() ),數列
),數列![]() 定義如下:對于正整數
定義如下:對于正整數![]() ,
, ![]() 是使得不等式
是使得不等式![]() 成立的所有
成立的所有![]() 中的最小值.
中的最小值.
(1)若![]() ,
, ![]() ,求
,求![]() ;
;
(2)若![]() ,
, ![]() ,求數列
,求數列![]() 的前
的前![]() 項和公式;
項和公式;
(3)是否存在![]() 和
和![]() ,使得
,使得![]()
![]() ?如果存在,求
?如果存在,求![]() 和
和![]() 的取值范圍;如果不存在,請說明理由.
的取值范圍;如果不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】將數列![]() 中的所有項按第一行排3項,以下每一行比上一行多一項的規則排成如下數表:
中的所有項按第一行排3項,以下每一行比上一行多一項的規則排成如下數表:
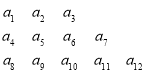
……
記表中的第一列數![]() ,
,![]() ,
,![]() ,…,構成數列
,…,構成數列![]() .
.
(1)設![]() ,求m的值;
,求m的值;
(2)若![]() ,對于任何
,對于任何![]() ,都有
,都有![]() ,且
,且![]() .求數列
.求數列![]() 的通項公式.
的通項公式.
(3)對于(2)中的數列![]() ,若上表中每一行的數按從左到右的順序均構成公比為q(
,若上表中每一行的數按從左到右的順序均構成公比為q(![]() )的等比數列,且
)的等比數列,且![]() ,求上表中第k(
,求上表中第k(![]() )行所有項的和
)行所有項的和![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】數列{2n﹣1}的前n項1,3,7,…,2n﹣1組成集合![]() (n∈N*),從集合An中任取k(k=1,2,3,…,n)個數,其所有可能的k個數的乘積的和為Tk(若只取一個數,規定乘積為此數本身),記Sn=T1+T2+…+Tn,例如當n=1時,A1={1},T1=1,S1=1;當n=2時,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,試寫出Sn=__.
(n∈N*),從集合An中任取k(k=1,2,3,…,n)個數,其所有可能的k個數的乘積的和為Tk(若只取一個數,規定乘積為此數本身),記Sn=T1+T2+…+Tn,例如當n=1時,A1={1},T1=1,S1=1;當n=2時,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,試寫出Sn=__.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知數列![]() 滿足:
滿足:![]() ,
,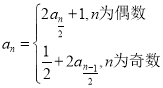 ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)設![]() ,求證:數列
,求證:數列![]() 是等比數列,并求出其通項公式;
是等比數列,并求出其通項公式;
(3)對任意的![]() ,
,![]() ,在數列
,在數列![]() 中是否存在連續的
中是否存在連續的![]() 項構成等差數列?若存在,寫出這
項構成等差數列?若存在,寫出這![]() 項,并證明這
項,并證明這![]() 項構成等差數列:若不存在,請說明理由.
項構成等差數列:若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,由半圓![]() 和部分拋物線
和部分拋物線![]() 合成的曲線
合成的曲線![]() 稱為“羽毛球開線”,曲線
稱為“羽毛球開線”,曲線![]() 與
與![]() 軸有
軸有![]() 兩個焦點,且經過點
兩個焦點,且經過點![]()

(1)求![]() 的值;
的值;
(2)設![]()
![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的最小值;
的最小值;
(3)過![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與“羽毛球形線”相交于點
與“羽毛球形線”相交于點![]() 三點,問是否存在實數
三點,問是否存在實數![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目: 來源: 題型:
【題目】經市場調查,某商品每噸的價格為![]() 萬元時,該商品的月供給量為
萬元時,該商品的月供給量為![]() 噸,
噸,![]() ;月需求量為
;月需求量為![]() 噸,
噸,![]() ,當該商品的需求量大于供給量時,銷售量等于供給量;當該商品的需求量不大于供給量時,銷售量等于需求量,該商品的月銷售額等于月銷售量與價格的乘積.
,當該商品的需求量大于供給量時,銷售量等于供給量;當該商品的需求量不大于供給量時,銷售量等于需求量,該商品的月銷售額等于月銷售量與價格的乘積.
(1)已知![]() ,若某月該商品的價格為x=7,求商品在該月的銷售額(精確到1元);
,若某月該商品的價格為x=7,求商品在該月的銷售額(精確到1元);
(2)記需求量與供給量相等時的價格為均衡價格,若該商品的均衡價格不低于每噸6萬元,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知![]() 定義在實數集
定義在實數集![]() 上的函數,把方程
上的函數,把方程![]() 稱為函數
稱為函數![]() 的特征方程,特征方程的兩個實根
的特征方程,特征方程的兩個實根![]() ,
,![]()
![]() 稱為
稱為![]() 的特征根.
的特征根.
(1)討論函數的奇偶性,并說明理由;
(2)求![]() 表達式;
表達式;
(3)把函數![]() ,
,![]() 的最大值記作
的最大值記作![]() 、最小值記作
、最小值記作![]() ,令
,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數![]() ,若在區間
,若在區間![]() 內有且只有一個實數
內有且只有一個實數![]() ,使得
,使得![]() 成立,則稱函數
成立,則稱函數![]() 在區間
在區間![]() 內具有唯一零點.
內具有唯一零點.
(1)判斷函數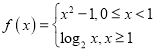 在區間
在區間![]() 內是否具有唯一零點,說明理由:
內是否具有唯一零點,說明理由:
(2)已知向量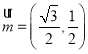 ,
,![]() ,
,![]() ,證明
,證明![]() 在區間
在區間![]() 內具有唯一零點.
內具有唯一零點.
(3)若函數![]() 在區間
在區間![]() 內具有唯一零點,求實數
內具有唯一零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com