精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

在直角坐標系中，曲線的參數方程為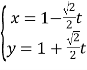（為參數），以坐標原點為極點，以軸正半軸為極軸建立極坐標系，曲線的極坐標方程為.

（1）求曲線的普通方程與曲線的直角坐標方程；

（2）若與交于兩點，點的極坐標為，求的值.

A.B.C.D.

【題目】設函數的圖象在處取得極值4.

（1）求函數的單調區間；

（2）對于函數，若存在兩個不等正數，，當時，函數的值域是，則把區間叫函數的“正保值區間”.問函數是否存在“正保值區間”，若存在，求出所有的“正保值區間”；若不存在，請說明理由.

【題目】已知函數.

（1）求函數的單調區間和極值；

（2）若，試討論函數的零點個數.

【題目】已知函數在區間上的最大值為9，最小值為1，記；

（1）求實數的值；

（2）若不等式成立，求實數的取值范圍；

（3）定義在上的函數，設，其中將區間任意劃分成個小區間，如果存在一個常數，使得和式恒成立，則稱函數為在上的有界變差函數，試判斷函數是否為在上的有界變差函數?若是，求的最小值；若不是，請說明理由.

【題目】某工廠在2016年的“減員增效”中對部分人員實行分流，規定分流人員第一年可以到原單位領取工資的100%，從第二年起，以后每年只能在原單位按上一年的領取工資，該廠根據分流人員的技術特長，計劃創辦新的經濟實體，該經濟實體預計第一年屬投資階段，第二年每人可獲得元收入，從第三年起每人每年的收入可在上一年的基礎上遞增50%，如果某人分流后工資的收入每年元，分流后進入新經濟實體，第年的收入為元；

（1）求的通項公式；

（2）當時，是否一定可以保證這個人分流一年后的收入永遠超過分流前的年收入?

【題目】已知函數．

（1）求函數的最小正周期；

（2）將函數的圖象向右平移個單位長度，再向下平移（）個單位長度后得到函數的圖象，且函數的最大值為2．

（ⅰ）求函數的解析式； （ⅱ）證明：存在無窮多個互不相同的正整數，使得．

【題目】已知橢圓的兩個焦點分別為，短軸的兩個端點分別為.

（Ⅰ）若為等邊三角形，求橢圓的方程；

（Ⅱ）若橢圓的短軸長為，過點的直線與橢圓相交于兩點，且，求直線的方程.

（1）已知在被抽取的女生中有6名高一（1）班學生，其中3名對游泳有興趣，現在從這6名學生中最忌抽取3人，求至少有2人對游泳有興趣的概率；

（2）該研究性學習小組在調查發現，對游泳有興趣的學生中有部分曾在市級以上游泳比賽中獲獎，如上表所示，若從高一（8）班和高一（9）班獲獎學生中隨機各抽取2人進行跟蹤調查.記選中的4人中市級以上游泳比賽獲獎的人數為，求隨機變量的分布列及數學期望.

【題目】在直角坐標系xOy中，直線l的參數方程為（t為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線C的極坐標方程為，直線l與曲線C交于不同的兩點A，B.

（1）求曲線C的參數方程；

（2）若點P為直線與x軸的交點，求的取值范圍.