Question

【題目】在信息快速發展的社會，“信息消費”已成為人們生活的重要組成部分．某高校組織課外小組在鄭州市的一個社區隨機抽取部分家庭，調查每月用于信息消費的金額，根據數據整理成如圖所示的不完整統計表和統計圖．已知A，B兩組戶數頻數直方圖的高度比為1：5． 月信息消費額分組統計表

組別	消費額（元）
A	10≤x＜100
B	100≤x＜200
C	20≤x＜300
D	300≤x＜400
E	x≥400

請結合圖表中相關數據解答下列問題：

（1）這次接受調查的有戶；
（2）在扇形統計圖中，“E”所對應的圓心角的度數是；
（3）請你補全頻數直方圖；
（4）若該社區有2000戶住戶，請估計月信息消費額不少于200元的戶數是多少？

Answer 1

【答案】
（1）50
（2）28.8°
（3）解：C組的頻數是：50×40%=20，如圖，

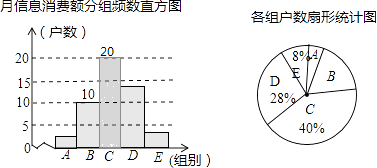
（4）解：2000×（28%+8%+40%）=1520（戶），

答：估計月信息消費額不少于200元的約有1520戶．

【解析】解：（1）A組的頻數是：10× =2； ∴這次接受調查的有（2+10）÷（1﹣8%﹣28%﹣40%）=50（戶），
故答案為：50；（2）“E”所對應的圓心角的度數是360°×8%=28.8°，
故答案為：28.8°；
（1）根據A、B兩組戶數直方圖的高度比為1：5，即兩組的頻數的比是1：5，據此即可求得A組的頻數；利用A和B兩組的頻數的和除以兩組所占的百分比即可求得總數；（2）用“E”組百分比乘以360°可得；（3）利用總數乘以百分比即可求得C組的頻數，從而補全統計圖；（4）利用總數2000乘以C、D、E的百分比即可．