
【題目】如圖,△PAD與正方形ABCD共用一邊AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,點E是棱PA的中點. 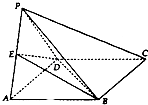
(1)求證:PC∥平面BDE;
(2)若直線PA與平面ABCD所成角為60°,求點A到平面BDE的距離.
【答案】
(1)證明:連接AC,交BD于O,連接EO,則
∵ABCD是正方形,
∴O是AC的中點,
∵點E是棱PA的中點,
∴PC∥OE,
∵OE平面BDE,BD平面BDE,
∴PC∥平面BDE
(2)解:取AD的中點N,連接PN,則
∵PA=PD,
∴PN⊥AD,
∵平面PAD∩平面ABCD=AD,
∴PN⊥平面ABCD,
∴∠PAN為直線PA與平面ABCD所成角∴∠PAN=60°∴PA=PD=AD=2,
∵AB⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴AB⊥平面PAD,
∴VB﹣DAE= ![]() =
= ![]() ,
,
Rt△EAB中,EA=1,AB=2,BE= ![]() ,
,
∵ ![]() ,BD=2
,BD=2 ![]() ,
,
∴DE⊥EB,
∴S△BDE= ![]() =
= ![]() .
.
設點A到平面BDE的距離為h.則 ![]() ,
,
∴h= ![]() ,
,
∴點A到平面BDE的距離為 ![]() .
.
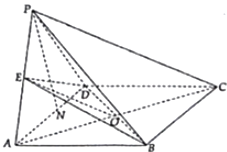
【解析】(1)連接AC,交BD于O,連接EO,證明PC∥OE,即可證明PC∥平面BDE;(2)取AD的中點N,連接PN,證明∠PAN為直線PA與平面ABCD所成角,利用等體積方法求點A到平面BDE的距離.
【考點精析】通過靈活運用直線與平面平行的判定,掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行即可以解答此題.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】定義在R上的偶函數f(x)滿足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是減函數,若α,β是銳角三角形的兩個內角,則( )
,且f(x)在[﹣3,﹣2]上是減函數,若α,β是銳角三角形的兩個內角,則( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計算題。
(1)已知等比數列{an}中,a1=﹣1,a4=64,求q與S4
(2)已知等差數列{an}中,a1= ![]() ,d=﹣
,d=﹣ ![]() ,Sn=﹣15,求n及an .
,Sn=﹣15,求n及an .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是首項為a1= ![]() ,公比q=
,公比q= ![]() 的等比數列,設bn+2=3
的等比數列,設bn+2=3 ![]() an(n∈N*),數列{cn}滿足cn=anbn .
an(n∈N*),數列{cn}滿足cn=anbn .
(1)求證:{bn}是等差數列;
(2)求數列{cn}的前n項和Sn;
(3)若cn≤ ![]() m2+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
m2+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和Sn= ![]() ,n∈N* .
,n∈N* .
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設bn= ![]() +(﹣1)nan , 求數列{bn}的前2n項和.
+(﹣1)nan , 求數列{bn}的前2n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E,F分別在BC,AD上,EF∥AB,現將四邊形ABEF沿EF折起,使得平面ABEF⊥平面EFDC. 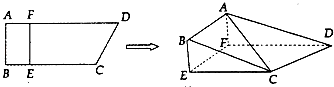
(1)若BE=3,求幾何體BEC﹣AFD的體積;
(2)求三棱錐A﹣CDF的體積的最大值,并求此時二面角A﹣CD﹣E的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場擬對某商品進行促銷,現有兩種方案供選擇,每種促銷方案都需分兩個月實施,且每種方案中第一個月與第二個月的銷售相互獨立.根據以往促銷的統計數據,若實施方案1,預計第一個月的銷量是促銷前的1.2倍和1.5倍的概率分別是0.6和0.4,第二個月的銷量是第一個月的1.4倍和1.6倍的概率都是0.5;若實施方案2,預計第一個月的銷量是促銷前的1.4倍和1.5倍的概率分別是0.7和0.3,第二個月的銷量是第一個月的1.2倍和1.6倍的概率分別是0.6和0.4.令![]() 表示實施方案
表示實施方案![]() 的第二個月的銷量是促銷前銷量的倍數.
的第二個月的銷量是促銷前銷量的倍數.
(Ⅰ)求![]() ,
, ![]() 的分布列;
的分布列;
(Ⅱ)不管實施哪種方案, ![]() 與第二個月的利潤之間的關系如下表,試比較哪種方案第二個月的利潤更大.
與第二個月的利潤之間的關系如下表,試比較哪種方案第二個月的利潤更大.
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的首項a1=a,Sn是數列{an}的前n項和,且滿足:Sn2=3n2an+Sn﹣12 , an≠0,n≥2,n∈N* .
(1)若數列{an}是等差數列,求a的值;
(2)確定a的取值集合M,使a∈M時,數列{an}是遞增數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com