【題目】如圖，三棱錐
中，
，底面
為正三角形．
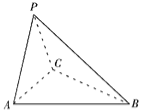
（Ⅰ）證明：
；
（Ⅱ）若平面
，
，
，求三棱錐
的體積．
【答案】（Ⅰ）詳見解析（Ⅱ）
【解析】
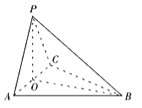
試題分析：（Ⅰ）證明線線垂直，一般通過線面垂直性質定理，即先證線面垂直，耳線面垂直的判定，往往從線線垂直出發，其中線線垂直的尋找與論證往往利用平幾知識：取
的中點
，則由等腰三角形性質得
，
，進而可證線面垂直
（Ⅱ）求三棱錐體積，關鍵在于確定高線，而高線的確定，主要利用線面垂直條件進行尋找，由（Ⅰ）得，即
為三棱錐
及
的高．根據面面垂直可得線面垂直，即
，所以
，最后代入錐的體積公式即可
試題解析：（Ⅰ）證明：取的中點，連接
，
，
∵
，
∴，
又
，
∴，
∴
．………………………………5分
（Ⅱ）平面
且交于
，
，
∴，即
為三棱錐
的高．
又
，
，
，
∴
，
∴
．
則三棱錐
的體積為．………………………………12分
科目：高中數學 來源： 題型：
【題目】為了調查中小學課外使用互聯網的情況，教育部向華東、華北、華南和西部地區60所中小學發出問卷
份， 
名學生參加了問卷調查，并根據所得數據畫出樣本的頻率分布直方圖（如圖）.
（1）要從這
名中小學中用分層抽樣的方法抽取
名中小學生進一步調查，則在
（小時）時間段內應抽出的人數是多少？
（2）若希望
的中小學生每天使用互聯網時間不少于
（小時），請估計
的值，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4
4：坐標系與參數方程
在直角坐標系
中，已知直線l1： 
（
， 
），拋物線C： 
（t為參數）．以原點
為極點， 
軸的非負半軸為極軸建立極坐標系．
（Ⅰ）求直線l1 和拋物線C的極坐標方程；
（Ⅱ）若直線l1 和拋物線C相交于點A（異于原點O），過原點作與l1垂直的直線l2，l2和拋物線C相交于點B（異于原點O），求△OAB的面積的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直角梯形
中， 
// 
， 
⊥
， 
⊥
, 點
是
邊的中點, 將△
沿
折起，使平面
⊥平面
，連接
, 
, 
, 得到如圖所示的幾何體.
（Ⅰ）求證： 
⊥平面
；
（Ⅱ）若
， 
，求二面角
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
