
【題目】如圖,四棱錐P﹣ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分別是棱AD,PC的中點 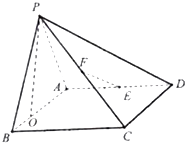
(1)求證:EF⊥平面PBC
(2)若直線PC與平面ABCD所成角為 ![]() ,點P在AB上的射影O在靠近點B的一側,求二面角P﹣EF﹣A的余弦值.
,點P在AB上的射影O在靠近點B的一側,求二面角P﹣EF﹣A的余弦值.
【答案】
(1)證明:取PB的中點G,連接AQ,FG,
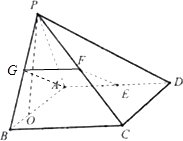
∵PA=AB,∴AG⊥PB,
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,BC⊥AB,
∴BC⊥平面PAB,
∴BC⊥AG,
∵PB∩BC=B,
∴AG⊥平面PBC
∵E、F分別是棱AD,PC的中點,
∴FG∥AE,FG=AE,
∴四邊形AEFG是平行四邊形,
∴EF∥AG,
∴EF⊥平面PBC
(2)解:作PO⊥AB=0,則PO⊥平面ABCD,
連接OC,則∠PCO= ![]() ,
,
∴PO=OC,設AO=x,則 ![]() =
= ![]() ,解得x=2,
,解得x=2,
以O為原點,建立空間直角坐標系,
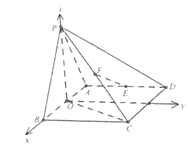
則P(0,0, ![]() ),A(﹣2,0,0),C(1,2,0),
),A(﹣2,0,0),C(1,2,0),
D(﹣2,2,0),E(﹣2,1,0),F( ![]() ),
),
![]() ,,
,,
設平面PEF的法向量 ![]() ,
,
則 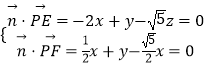 ,取x=1,得
,取x=1,得 ![]() =(1,﹣3,﹣
=(1,﹣3,﹣ ![]() ),
),
設平面AEF的法向量 ![]() ,
,
∵ ![]() ,
,
∴  ,取a=1,得
,取a=1,得 ![]() ,
,
設二面角P﹣EF﹣A的平面角為α,
則cosα=|coss< ![]() >|=|
>|=| ![]() |=
|= ![]() .
.
∴二面角P﹣EF﹣A的余弦值為 ![]() .
.
【解析】(1)取PB的中點G,連接AQ,FG,則AG⊥PB,BC⊥AB,從而BC⊥平面PAB,BC⊥AG,由此能證明EF⊥平面PBC.(2)作PO⊥AB=0,連接OC,以O為原點,建立空間直角坐標系,利用向量法能求出二面角P﹣EF﹣A的余弦值.
【考點精析】根據題目的已知條件,利用直線與平面垂直的判定和空間角的異面直線所成的角的相關知識可以得到問題的答案,需要掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則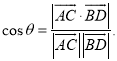 .
.


科目:高中數學 來源: 題型:
【題目】正方體ABCD﹣A1B1C1D1中,點M,N分別在線段AB1、BC1上,且AM=BN.以下結論:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN與A1C1異面,⑤MN與 A1C1成30°.其中有可能成立的結論的個數為( ) 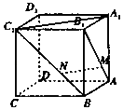
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第96屆(春季)全國糖酒商品交易會于2017年3月23日至25日在四川舉辦.展館附近一家川菜特色餐廳為了研究參會人數與本店所需原材料數量的關系,在交易會前查閱了最近5次交易會的參會人數![]() (萬人)與餐廳所用原材料數量
(萬人)與餐廳所用原材料數量![]() (袋),得到如下數據:
(袋),得到如下數據:

(Ⅰ)請根據所給五組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅱ)若該店現有原材料12袋,據悉本次交易會大約有13萬人參加,為了保證原材料能夠滿足需要,則該店應至少再補充原材料多少袋?
(參考公式:  ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小區提倡低碳生活,環保出行,在小區提供自行車出租.該小區有40輛自行車供小區住戶租賃使用,管理這些自行車的費用是每日92元,根據經驗,若每輛自行車的日租金不超過5元,則自行車可以全部出租,若超過5元,則每超過1元,租不出的自行車就增加2輛,為了便于結算,每輛自行車的日租金x元只取整數,用f(x)元表示出租自行車的日純收入(日純收入=一日出租自行車的總收入﹣管理費用)
(1)求函數f(x)的解析式及其定義域;
(2)當租金定為多少時,才能使一天的純收入最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直線PA垂直于圓O所在的平面,△ABC內接于圓O,且AB為圓O的直徑,點M為線段PB的中點.現有以下命題:①BC⊥PC;②OM∥平面APC;③點B到平面PAC的距離等于線段BC的長.其中真命題的個數為( ) 
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲,乙,丙,丁四位同學課余參加巴蜀愛心社和巴蜀文學風的活動,每人參加且只能參加一個社團的活動,并且參加每個社團都是等可能的.
(1)求巴蜀愛心社和巴蜀文學風都至少有1人參加的概率;
(2)求甲,乙在同一個社團,丙,丁不在同一個社團的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com