
【題目】(選修4﹣5:不等式選講)
已知函數(shù)f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)當a=﹣2時,求不等式f(x)<g(x)的解集;
(2)設(shè)a>﹣1,且當 ![]() 時,f(x)≤g(x),求a的取值范圍.
時,f(x)≤g(x),求a的取值范圍.
【答案】
(1)解:當a=﹣2時,求不等式f(x)<g(x)化為|2x﹣1|+|2x﹣2|﹣x﹣3<0.
設(shè)y=|2x﹣1|+|2x﹣2|﹣x﹣3,則 y= 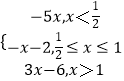 ,它的圖象如圖所示:
,它的圖象如圖所示:
結(jié)合圖象可得,y<0的解集為(0,2),故原不等式的解集為(0,2).
(2)解:設(shè)a>﹣1,且當 ![]() 時,f(x)=1+a,不等式化為 1+a≤x+3,故 x≥a﹣2對
時,f(x)=1+a,不等式化為 1+a≤x+3,故 x≥a﹣2對 ![]() 都成立.
都成立.
故﹣ ![]() ≥a﹣2,解得 a≤
≥a﹣2,解得 a≤ ![]() ,故a的取值范圍為(﹣1,
,故a的取值范圍為(﹣1, ![]() ].
].
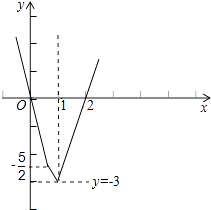
【解析】(1)當a=﹣2時,求不等式f(x)<g(x)化為|2x﹣1|+|2x﹣2|﹣x﹣3<0.設(shè)y=|2x﹣1|+|2x﹣2|﹣x﹣3,畫出函數(shù)y的圖象,數(shù)形結(jié)合可得結(jié)論.(2)不等式化即 1+a≤x+3,故 x≥a﹣2對 ![]() 都成立.故﹣
都成立.故﹣ ![]() ≥a﹣2,由此解得a的取值范圍.
≥a﹣2,由此解得a的取值范圍.
【考點精析】本題主要考查了函數(shù)單調(diào)性的性質(zhì)和絕對值不等式的解法的相關(guān)知識點,需要掌握函數(shù)的單調(diào)區(qū)間只能是其定義域的子區(qū)間 ,不能把單調(diào)性相同的區(qū)間和在一起寫成其并集;含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規(guī)律:關(guān)鍵是去掉絕對值的符號才能正確解答此題.


 新課標快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案
新課標快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() ,其中a為實數(shù).
,其中a為實數(shù).
(1)當 ![]() 時,求曲線y=f(x)在點(1,f(1))處的切線方程;
時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)當x≥ ![]() 時,若關(guān)于x的不等式f(x)≥0恒成立,試求a的取值范圍.
時,若關(guān)于x的不等式f(x)≥0恒成立,試求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知以M為圓心的圓M: ![]() 及其上一點A(2,4)
及其上一點A(2,4)
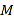
(1)設(shè)圓N與x軸相切,與圓M外切,且圓心N在直線x=6上,求圓N的標準方程;
(2)設(shè)平行于OA的直線l與圓M相交于B、C兩點,且BC=OA,求直線l的方程;
(3)設(shè)點T(t,o)滿足:存在圓M上的兩點P和Q,使得![]() ,求實數(shù)t的取值范圍。
,求實數(shù)t的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線M: ![]() =1(a>0,b>0)的上焦點為F,上頂點為A,B為虛軸的端點,離心率e=
=1(a>0,b>0)的上焦點為F,上頂點為A,B為虛軸的端點,離心率e= ![]() ,且S△ABF=1﹣
,且S△ABF=1﹣ ![]() .拋物線N的頂點在坐標原點,焦點為F.
.拋物線N的頂點在坐標原點,焦點為F.
(1)求雙曲線M和拋物線N的方程;
(2)設(shè)動直線l與拋物線N相切于點P,與拋物線的準線相交于點Q,則以PQ為直徑的圓是否恒過y軸上的一個定點?如果經(jīng)過,試求出該點的坐標,如果不經(jīng)過,試說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() ,若對于任意
,若對于任意![]() 數(shù)列
數(shù)列![]() 滿足
滿足![]() ,則稱數(shù)列
,則稱數(shù)列![]() 為“
為“![]() 數(shù)列”.
數(shù)列”.
(Ⅰ)已知數(shù)列:![]() ,
,![]() ,
,![]() 是“
是“![]() 數(shù)列”,求實數(shù)
數(shù)列”,求實數(shù)![]() 的取值范圍.
的取值范圍.
(Ⅱ)是否存在首項為![]() 的等差數(shù)列
的等差數(shù)列![]() 為“
為“![]() 數(shù)列”,且前
數(shù)列”,且前![]() 項和
項和![]() 滿足
滿足![]() ,若存在,求出
,若存在,求出![]() 的通項公式,若不存在,請說明理由;
的通項公式,若不存在,請說明理由;
(Ⅲ)已知各項均為正整數(shù)的等比數(shù)列![]() 是“
是“![]() 數(shù)列”,數(shù)列
數(shù)列”,數(shù)列![]() 不是“
不是“![]() 數(shù)列”,若數(shù)列
數(shù)列”,若數(shù)列![]() ,試判斷數(shù)列
,試判斷數(shù)列![]() 是否“
是否“![]() 數(shù)列”,并且說明理由.
數(shù)列”,并且說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)y= ![]() x2的圖象在點(x0 ,
x2的圖象在點(x0 , ![]() x02)處的切線為l,若l也為函數(shù)y=lnx(0<x<1)的圖象的切線,則x0必須滿足( )
x02)處的切線為l,若l也為函數(shù)y=lnx(0<x<1)的圖象的切線,則x0必須滿足( )
A.![]() <x0<1
<x0<1
B.1<x0< ![]()
C.![]() <x0<
<x0< ![]()
D.![]() <x0<2
<x0<2
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】自2017年2月底,90多所自主招生試點高校將陸續(xù)出臺2017年自主招生簡章,某校高三年級選取了在期中考試中成績優(yōu)異的100名學(xué)生作為調(diào)查對象,對是否準備參加2017年的自主招生考試進行了問卷調(diào)查,其中“準備參加”“不準備參加”和“待定”的人數(shù)如表:
準備參加 | 不準備參加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有參加調(diào)查的同學(xué)中,在三種類型中用分層抽樣的方法抽取20人進行座談交流,則在“準備參加”“不準備參加”和“待定”的同學(xué)中應(yīng)各抽取多少人?
(2)在“準備參加”的同學(xué)中用分層抽樣方法抽取6人,從這6人中任意抽取2人,求至少有一名女生的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com