
【題目】已知函數(shù)f(x)= ![]() -lnx-
-lnx-![]() .
.
(Ⅰ)求曲線y=f(x)在點(diǎn)(1,f(1))處的切線方程;
(Ⅱ)求證:lnx≥-![]()
(Ⅲ)判斷曲線y=f(x)是否位于x軸下方,并說明理由.
【答案】(Ⅰ)(![]() -1)x-y-
-1)x-y-![]() +1=0;(Ⅱ)見解析;(Ⅲ)見解析.
+1=0;(Ⅱ)見解析;(Ⅲ)見解析.
【解析】試題分析:(Ⅰ)函數(shù)求導(dǎo)得切線斜率為f’(1)= ![]() -1,再利用直線的點(diǎn)斜式求解即可;
-1,再利用直線的點(diǎn)斜式求解即可;
(Ⅱ)要證明lnx≥-![]() ,(x>0)”等價(jià)于“xlnx≥-
,(x>0)”等價(jià)于“xlnx≥-![]() ”,設(shè)函數(shù)g(x)=xlnx,求導(dǎo)結(jié)合單調(diào)性得g(
”,設(shè)函數(shù)g(x)=xlnx,求導(dǎo)結(jié)合單調(diào)性得g(![]() )
)![]() 即可證得;
即可證得;
(Ⅲ)由(Ⅱ)可知lnx≥![]() ,所以f(x)≤
,所以f(x)≤![]() -
-![]() (
(![]() ),求導(dǎo)結(jié)合單調(diào)性得k(x)≤k(1)=0恒成立,即可證得.
),求導(dǎo)結(jié)合單調(diào)性得k(x)≤k(1)=0恒成立,即可證得.
試題解析:
函數(shù)的定義域?yàn)?/span>(0,+∞),
f’(x)=- ![]() -
-![]() +
+![]()
(Ⅰ)f’(1)= ![]() -1,又f(1)=-
-1,又f(1)=- ![]()
曲線y=f(x)在x=1處的切線方程為
y+![]() =(
=(![]() -1)x-
-1)x-![]() +1.
+1.
即(![]() -1)x-y-
-1)x-y-![]() +1=0.
+1=0.
(Ⅱ)“要證明lnx≥-![]() ,(x>0)”等價(jià)于“xlnx≥
,(x>0)”等價(jià)于“xlnx≥![]()
設(shè)函數(shù)g(x)=xlnx.
令g’(x)=1+lnx=0,解得![]() .
.
x | (0, |
| ( |
g(x) | - | 0 | + |
g(x) | 遞減 |
| 遞增 |
因此,函數(shù)g(x)的最小值為g(![]() )=-
)=-![]() ,故xlnx≥
,故xlnx≥![]() .
.
即lnx≥![]() .
.
(Ⅲ)曲線y=f(x)位于x軸下方.理由如下:
由(Ⅱ)可知lnx≥![]() ,所以f(x)≤
,所以f(x)≤![]() -
-![]() =
=![]() (
(![]() ).
).
設(shè)k(x)= ![]() ,則k’(x)=
,則k’(x)= ![]()
令k’(x)>0得0<x<1;令k’(x)<0得x>1.
所以k(x)在(0,1)上為增函數(shù),(1,+∞)上為減函數(shù).
所以當(dāng)x>0時(shí),k(x)≤k(1)=0恒成立,當(dāng)且僅當(dāng)x=1時(shí),k(1)=0.
又因?yàn)?/span>f(1)=- ![]() <0,所以f(x)<0恒成立.
<0,所以f(x)<0恒成立.
故曲線y=f(x)位于x軸下方.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)f(x)的最小值為-4,且關(guān)于x的不等式f(x)≤0的解集為{x|-1≤x≤3,x∈R}.
(1)求函數(shù)f(x)的解析式;
(2)求函數(shù)![]() 的零點(diǎn)個(gè)數(shù).
的零點(diǎn)個(gè)數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(I)若![]() ,求曲線
,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(II)討論函數(shù)![]() 在
在![]() 上的單調(diào)性;
上的單調(diào)性;
(III)若存在![]() ,使得
,使得![]() 成立,求實(shí)數(shù)a的取值范圍。
成立,求實(shí)數(shù)a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)有一個(gè)正方形網(wǎng)格,其中每個(gè)最小正方形的邊長都為5 cm.現(xiàn)用直徑為2 cm的硬幣投擲到此網(wǎng)格上,求硬幣落下后與格線有公共點(diǎn)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將集合M={1,2,3,...,15}表示為它的5個(gè)三元子集(三元集:含三個(gè)元素的集合)的并集,并且這些三元子集的元素之和都相等,則每個(gè)三元集的元素之和為________;請(qǐng)寫出滿足上述條件的集合M的5個(gè)三元子集__________(只寫出一組)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)若![]() ,證明:函數(shù)
,證明:函數(shù)![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
(Ⅱ)是否存在實(shí)數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 在
在![]() 內(nèi)存在兩個(gè)極值點(diǎn)?若存在,求實(shí)數(shù)
內(nèi)存在兩個(gè)極值點(diǎn)?若存在,求實(shí)數(shù)![]() 的取值范圍;若不存在,請(qǐng)說明理由. (參考數(shù)據(jù):
的取值范圍;若不存在,請(qǐng)說明理由. (參考數(shù)據(jù): ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,曲線
,曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程為
處的切線方程為![]() 。
。
(1)求![]() 、
、![]() 的值;
的值;
(2)如果當(dāng)![]() ,且
,且![]() 時(shí),
時(shí), ![]() ,求
,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
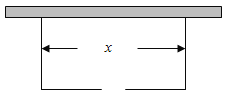
【題目】圍建一個(gè)面積為360![]() 的矩形場(chǎng)地,要求矩形場(chǎng)地的一面利用舊墻(利用舊墻需維修),其它三面圍墻要新建,在舊墻的對(duì)面的新墻上要留一個(gè)寬度為2m的進(jìn)出口,如圖所示,已知舊墻的維修費(fèi)用為45元/m,新墻的造價(jià)為180元/m,設(shè)利用的舊墻的長度為
的矩形場(chǎng)地,要求矩形場(chǎng)地的一面利用舊墻(利用舊墻需維修),其它三面圍墻要新建,在舊墻的對(duì)面的新墻上要留一個(gè)寬度為2m的進(jìn)出口,如圖所示,已知舊墻的維修費(fèi)用為45元/m,新墻的造價(jià)為180元/m,設(shè)利用的舊墻的長度為![]() (單位:
(單位:![]() ),修建此矩形場(chǎng)地圍墻的總費(fèi)用為
),修建此矩形場(chǎng)地圍墻的總費(fèi)用為![]() (單位:元)
(單位:元)
(1)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)試確定![]() ,使修建此矩形場(chǎng)地圍墻的總費(fèi)用最小,并求出最小總費(fèi)用。
,使修建此矩形場(chǎng)地圍墻的總費(fèi)用最小,并求出最小總費(fèi)用。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形AMDE的邊長為2,B,C分別為AM,MD的中點(diǎn).在五棱錐P-ABCDE中,F為棱PE的中點(diǎn),平面ABF與棱PD,PC分別交于點(diǎn)G,H.
(1)求證:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE.求直線BC與平面ABF所成角的大小,并求線段PH的長.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com