
2007年杭州市第一次高考科目教學質量檢測
數學試題卷(文科)
考生須知:
1. 本卷滿分150分, 考試時間120分鐘.
2. 答題前, 在答題卷密封區內填寫學校、班級和姓名.
3. 所有答案必須寫在答題卷上, 寫在試題卷上無效.
4. 考試結束, 只需上交答題卷.
參考公式
如果事件 互斥,那么
互斥,那么 ;
;
如果事件 相互獨立,那么
相互獨立,那么 ;
;
如果事件 在一次試驗中發生的概率是
在一次試驗中發生的概率是 ,那么
,那么 次獨立重復試驗中恰好發生
次獨立重復試驗中恰好發生 次的概率
次的概率 .
.
一. 選擇題 : 本大題共10小題, 每小題5分, 共50分. 在每小題給出的四個選項中, 只有一項是符合題目要求的 .
1. 以下4組函數中, 表示同一函數的是 ( )
(A)  (B)
(B)

 2.
某校為了了解學生的課外閱讀情況,隨
2.
某校為了了解學生的課外閱讀情況,隨
機調查了50名學生,得到他們在某一天各
自課外閱讀所用時間的數據,結果用右側
的條形圖表示. 根據條形圖可得這50名學
生這一天平均每人的課外閱讀時間為 ( )
(第2題)
(A) 0.6小時 (B) 0.9小時
(C) 1.0小時 (D) 1.5小時
3. 記函數 的反函數為
的反函數為 ,則
,則 ( )
( )
(A) 2 (B) -2 (C) 3 (D) -3
4. 設數列 是等差數列, 且
是等差數列, 且 是數列
是數列 的前
的前 項的和, 則有
項的和, 則有
( )
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
5. 已知 , 則
, 則 的最小值為 ( )
的最小值為 ( )
(A) 6 (B) 7 (C) 8 (D) 9
6. 已知| a | = 3,
| b | = 4,
(a +
b)?( a +3 b) = 33, 則a與b的夾角 為 ( )
為 ( )
(A)  (B)
(B)
 (C)
(C)
 (D)
(D)

7. 給出四個函數分別滿足: ①  ; ②
; ②  ;
;
③  ; ④
; ④  . 與下列函數圖象相對應的是
. 與下列函數圖象相對應的是
( )


(第7題)
(A) ① ②
② ③
③ ④
④ (B) ①
(B) ① ②
② ③
③ ④
④
(C) ① ②
② ③
③ ④
④ (D) ①
(D) ① ②
② ③
③ ④
④
8. 設兩個獨立事件 都不發生的概率為
都不發生的概率為 ,
,  發生
發生 不發生的概率與
不發生的概率與 發生
發生 不發生的概率相等, 那么
不發生的概率相等, 那么 為 ( )
為 ( )
(A)  (B)
(B)
 (C)
(C)  (D)
(D)

9.已知曲線 ,則過點
,則過點 的切線方程是 ( )
的切線方程是 ( )
(A)  (B)
(B) 
(C)  (D)
(D) 
10.
定義在R上的偶函數 滿足
滿足 ,當
,當 ∈[3,4]時,
∈[3,4]時, ,則有 ( )
,則有 ( )
(C)  (D)
(D)

二.填空題: 本大題有4小題, 每小題4分, 共16分. 把答案填在答題卷的相應位置.
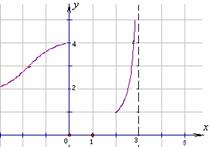
(第11題)
11. 函數 的圖象如右所示.
的圖象如右所示.
那么,  的定義域是 ________ ; 值域是
的定義域是 ________ ; 值域是
__________ ; 其中只與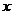 的一個值對應的
的一個值對應的 值的范圍是 ________________ .
值的范圍是 ________________ .
12. 已知角 的終邊在直線
的終邊在直線 上,
上,
則 的值是 __________ .
的值是 __________ .
13. 一個總體中有100個個體,隨機編號0,1,2,…,99,依編號順序平均分成10個
小組,組號依次為1,2,3,…,10. 現用系統抽樣方法抽取一個容量為10的樣本,規
定如果在第1組隨機抽取的號碼為 ,那么在第
,那么在第 組中抽取的號碼個位數字與
組中抽取的號碼個位數字與 的
的
個位數字相同,若 ,則在第7組中抽取的號碼是
.
,則在第7組中抽取的號碼是
.
14. 一個不懂英語的小孩用寫有
“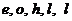 ” 5個英語字母的卡片拼成單詞“
” 5個英語字母的卡片拼成單詞“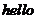 ”, 那么可能是錯誤的拼法(卡片不橫放也不顛倒)共有 _____ 種.
”, 那么可能是錯誤的拼法(卡片不橫放也不顛倒)共有 _____ 種.
三. 解答題: 本大題有6小題, 每小題14分,共84分. 解答應寫出文字說明, 證明過程或演算步驟.
15. (本小題滿分14分)
已知集合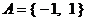 ,
, 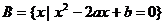 , 若
, 若 且
且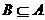 , 求
, 求
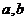 的值.
的值.
16. (本小題滿分14分)
設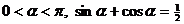 , 求
, 求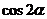 的值.
的值.
17.(本小題滿分14分)
已知數列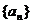 的前
的前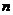 項和
項和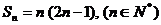 .
.
(1)
求數列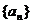 的通項公式,并證明該數列為等差數列;
的通項公式,并證明該數列為等差數列;
(2)
設數列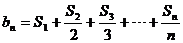
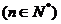 , 試判定: 是否存在自然數
, 試判定: 是否存在自然數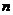 ,
,
使得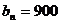 ,若存在, 求出
,若存在, 求出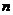 的值;若不存在,說明理由.
的值;若不存在,說明理由.
18 . (本小題滿分14分)
已知函數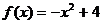 ,設函數
,設函數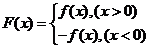 .
.
(1)求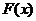 表達式;
表達式;
(2)解不等式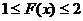 ;
;
(3)設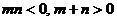 , 判斷
, 判斷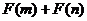 能否小于0 ?
能否小于0 ?
19. (本小題滿分14分)
杭州風景區有一家自行車租車公司,公司設有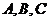 三個營業站,顧客可以從任何一處營業站租車,并在任何一處營業站還車. 根據統計發現租車處與還車處有如下的規律性:
三個營業站,顧客可以從任何一處營業站租車,并在任何一處營業站還車. 根據統計發現租車處與還車處有如下的規律性:
1) 在 站租車者有30%在
站租車者有30%在 站還車,20%在
站還車,20%在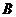 站還車,50%在
站還車,50%在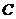 站還車;
站還車;
2) 在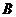 站租車者有70%在
站租車者有70%在 站還車,10%在
站還車,10%在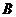 站還車,20%在
站還車,20%在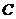 站還車;
站還車;
記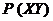 表示 “某車由
表示 “某車由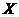 站租出還至
站租出還至 站的概率”,
站的概率”, 表示 “某車由
表示 “某車由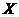 站租出還至
站租出還至 站, 再由
站, 再由 站還至
站還至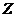 站的概率”. 按以上約定的規則,
站的概率”. 按以上約定的規則,
(1) 求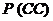 ;
;
(2) 求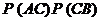 ;
;
(3) 設某輛自行車從 站租出,求此車歸還至某站再次出租后,回到
站租出,求此車歸還至某站再次出租后,回到 站的概率
站的概率 .
.
20. (本小題滿分14分)
設函數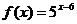 ,
, 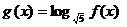
(1)
解不等式
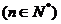 ;
;
(2)
求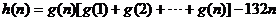
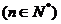 的最小值.
的最小值.
2007年杭州市第一次高考科目教學質量檢測
數學參考評分標準(文科)
一. 選擇題 : (本大題共10小題, 每小題5分, 共50分)
題號
1
2
3
4
5
6
7
8
9
10
答案
A
B
B
A
D
D
B
A
C
二.填空題: (本大題有4小題, 每小題4分, 共16分)
11. 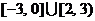 ; [1,5];
; [1,5];  . (端點相對應為開也可, 左, 上為無窮也可)
. (端點相對應為開也可, 左, 上為無窮也可)
12.  或
或 13. 63 14.
59
13. 63 14.
59
三. 解答題: (本大題有6小題, 每小題14分,共84分)
15. (本小題滿分14分)
因為 , 且
, 且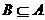 , 所以
, 所以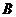 有兩種存在情況:
有兩種存在情況:
(1) 當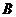 含有兩個元素時,
含有兩個元素時, 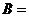
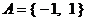 , 易得
, 易得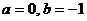 ;
--- 4分
;
--- 4分
(2) 當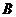 含有一個元素時, 由
含有一個元素時, 由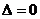 , 得
, 得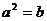 ,
--- 2分
,
--- 2分
若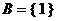 時, 由
時, 由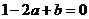 , 得
, 得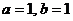 ;
---
4分
;
---
4分
若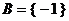 時, 由
時, 由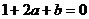 , 得
, 得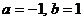 .
--- 4分
.
--- 4分
16. (本小題滿分14分)
由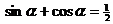 , 可得
, 可得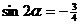 --- 5分
--- 5分
但由條件又知應該有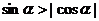 , 即
, 即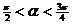 , ∴
, ∴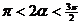 ,
--- 4分
,
--- 4分
∴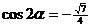 .
--- 5分
.
--- 5分
17.(本小題滿分14分)
(1)
當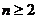 時,
時,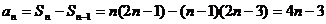 ,
--- 4分
,
--- 4分
當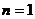 時,
時, 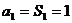 , 適合, ∴
, 適合, ∴ 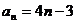 ,
--- 2分
,
--- 2分
而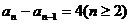 ,所以
,所以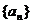 為等差數列.
--- 2分
為等差數列.
--- 2分
(2)
∵ 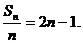 , ---
2分
, ---
2分
∴ 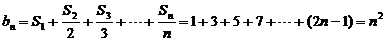 ,
--- 2分
,
--- 2分
由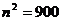 , 得
, 得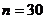 , 即存在滿足條件的自然數為30.
--- 2分
, 即存在滿足條件的自然數為30.
--- 2分
18 . (本小題滿分14分)
(1) 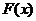 =
= 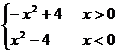 ;
--- 2分
;
--- 2分
當 時, 解不等式 1 £
時, 解不等式 1 £ 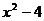 £ 2, 得 ?
£ 2, 得 ?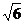 £
£ 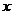 £ ?
£ ?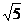 .
--- 2分
.
--- 2分
綜合上述不等式的解為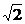 £
£ 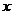 £
£ 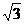 或?
或?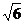 £
£ 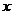 £ ?
£ ?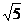 .
--- 2分
.
--- 2分
(3)∵ 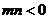 , 不妨設
, 不妨設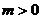 , 則
, 則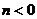 , 又
, 又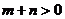 , ∴
, ∴ 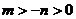 ,
,
∴  , ---
2分
, ---
2分
∴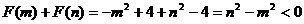 ,
,
即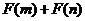 能小于0.
--- 4分
能小于0.
--- 4分
19.(本小題滿分14分)
(1) 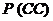 = 0.1;
---
4分
= 0.1;
---
4分
(2)  ;
--- 4分
;
--- 4分
(3) 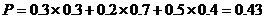 .
--- 6分
.
--- 6分
20. (本小題滿分14分)
(1)  ,
--- 2分
,
--- 2分
∴  ,
--- 2分
,
--- 2分
解不等式 , 得
, 得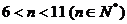 ;
--- 2分
;
--- 2分
(2) 當 時,
時,  ,
,
--- 2分
∵  , ∴
, ∴  時,
時,  單調遞減,
單調遞減, 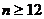 時,
時,  單調遞增, --- 2分
單調遞增, --- 2分
當 時,
時, 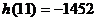 , 當
, 當 時,
時, 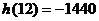 ,
,
∴  .
---
2分
.
---
2分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com