
3.概念辨析:為使大家鞏固傾斜角和斜率的概念,我們來看下面的題.
關于直線的傾斜角和斜率,下列哪些說法是正確的:
A.任一條直線都有傾斜角,也都有斜率;
B.直線的傾斜角越大,它的斜率就越大;
C.平行于 軸的直線的傾斜角是0或π;
軸的直線的傾斜角是0或π;
D.兩直線的傾斜角相等,它們的斜率也相等.
E.直線斜率的范圍是(-∞,+∞).
辨析:上述說法中,E正確,其余均錯誤,原因是:A.與x軸垂直的直線傾斜角為 ,但斜率不存在;B.舉反例說明,120°>30°,但
,但斜率不存在;B.舉反例說明,120°>30°,但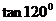 =-
=-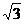 <
<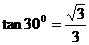 ;C.平行于
;C.平行于 軸的直線的傾斜角為0;D.如果兩直線的傾斜角都是
軸的直線的傾斜角為0;D.如果兩直線的傾斜角都是 ,但斜率不存在,也就談不上相等.
,但斜率不存在,也就談不上相等.
說明:①當直線和 軸平行或重合時,我們規定直線的傾斜角為0°;②直線傾斜角的取值范圍是
軸平行或重合時,我們規定直線的傾斜角為0°;②直線傾斜角的取值范圍是 ;③傾斜角是90°的直線沒有斜率.
;③傾斜角是90°的直線沒有斜率.
2.直線的傾斜角與斜率:在平面直角坐標系中,對于一條與 軸相交的直線,如果把
軸相交的直線,如果把 軸繞著交點按逆時針方向旋轉到和直線重合時所轉的最小正角記為
軸繞著交點按逆時針方向旋轉到和直線重合時所轉的最小正角記為 ,那么
,那么 就叫做直線的傾斜角.
就叫做直線的傾斜角.
當直線和 軸平行或重合時,我們規定直線的傾斜角為0°
軸平行或重合時,我們規定直線的傾斜角為0° 因此,根據定義,我們可以得到傾斜角的取值范圍是0°≤
因此,根據定義,我們可以得到傾斜角的取值范圍是0°≤ <180°
<180°
傾斜角不是90°的直線,它的傾斜角的正切叫做這條直線的斜率,常用 表示. 傾斜角是
表示. 傾斜角是 的直線沒有斜率
的直線沒有斜率
1.直線方程的概念:以一個方程的解為坐標的點都是某條直線上的點,反過來,這條直線上的點的坐標都是這個方程的解,這時,這個方程就叫做這條直線的方程,這條直線叫做這個方程的直線
在平面直角坐標系中研究直線時,就是利用直線與方程的這種關系,建立直線的方程的概念,并通過方程來研究直線的有關問題.為此,我們先研究直線的傾斜角和斜率
3.這兩點與函數式的關系:這兩點就是滿足函數式的兩對 值.
值.
因此,我們可以得到這樣一個結論:一般地,一次函數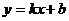 的圖象是一條直線,它是以滿足
的圖象是一條直線,它是以滿足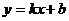 的每一對
的每一對 的值為坐標的點構成的.
的值為坐標的點構成的.
由于函數式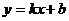 也可以看作二元一次方程.所以我們可以說,這個方程的解和直線上的點也存在這樣的對應關系.
也可以看作二元一次方程.所以我們可以說,這個方程的解和直線上的點也存在這樣的對應關系.
有了上述基礎,我們也就不難理解“直線的方程”和“方程的直線”的基本概念
2.對于一給定函數 ,作出它的圖象的方法:由于兩點確定一條直線,所以在直線上任找兩點即可.
,作出它的圖象的方法:由于兩點確定一條直線,所以在直線上任找兩點即可.
在初中,我們已經學習過一次函數,并接觸過一次函數的圖象,現在,請同學們作一下回顧:
1.一次函數的圖象特點:一次函數形如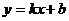 ,它的圖象是一條直線.
,它的圖象是一條直線.
1 若cosx=0,則角x等于( )
若cosx=0,則角x等于( )
A.kπ,(k∈Z)
B.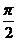 +kπ,(k∈Z)
+kπ,(k∈Z)
C.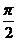 +2kπ,(k∈Z) D.-
+2kπ,(k∈Z) D.-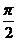 +2kπ,(k∈Z)
+2kπ,(k∈Z)
2 若tanx=0,則角x等于( )
若tanx=0,則角x等于( )
A.kπ,(k∈Z)
B.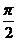 +kπ,(k∈Z)
+kπ,(k∈Z)
C.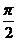 +2kπ,(k∈Z) D.-
+2kπ,(k∈Z) D.-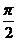 +2kπ,(k∈Z)
+2kπ,(k∈Z)
3 已知cosx=-
已知cosx=-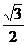 ,π<x<2π,則x等于( )
,π<x<2π,則x等于( )
A.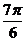 B.
B.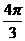 C.
C. D.
D.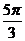
4 若tan(3π-x)=-
若tan(3π-x)=-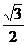 ,則x=
,則x=

5 滿足tanx=
滿足tanx= 的x的集合為
的x的集合為 
6 在閉區間[0,2π]上,適合關系式cosx=-0.4099的角有 個,用0.4099的反余弦表示的x值是
___________;用-0
在閉區間[0,2π]上,適合關系式cosx=-0.4099的角有 個,用0.4099的反余弦表示的x值是
___________;用-0 4099的反余弦表示的x的值是
_________
4099的反余弦表示的x的值是
_________
例1
(1)已知 ,求x(精確到
,求x(精確到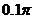 )
)
解:在區間 上
上 是增函數,符合條件的角是唯一的
是增函數,符合條件的角是唯一的

(2)已知 且
且 ,求x的取值集合
,求x的取值集合
解: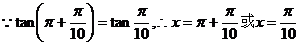
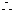 所求的x的集合是
所求的x的集合是 (即
(即 )
)
(3)已知 ,求x的取值集合
,求x的取值集合
解:由上題可知: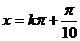 ,
,
合并為
例2已知 ,根據所給范圍求
,根據所給范圍求 :
:
1° 為銳角 2°
為銳角 2° 為某三角形內角 3°
為某三角形內角 3° 為第二象限角 4°
為第二象限角 4°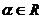
解:1°由題設
2°設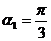 ,或
,或
3°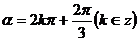
4°由題設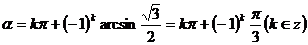
例3 求適合下列關系的x的集合
1°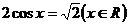 2°
2° 3°
3°
解:1°
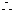 所求集合為
所求集合為
2° 所求集合為
所求集合為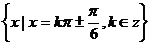
3°
例4 直角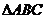 銳角A,B滿足:
銳角A,B滿足: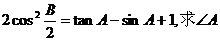
解:由已知:
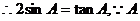 為銳角,
為銳角,
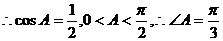
例5 1°用反三角函數表示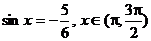 中的角x
中的角x
2°用反三角函數表示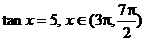 中的角x
中的角x
解:1° ∵ ∴
∴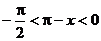
又由 得
得
∴ ∴
∴
2° ∵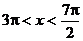 ∴
∴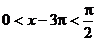
又由 得
得
∴ ∴
∴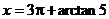
例6已知 ,求角x的集合
,求角x的集合
解:∵ ∴
∴
由 得
得 
由 得
得 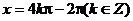
故角x的集合為
例7求 的值
的值
解:arctan2 = a, arctan3 = b 則tana = 2, tanb = 3
且 ,
, 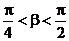
∴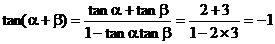
而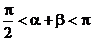 ∴a + b =
∴a + b = 
又arctan1
=  ∴
∴ = p
= p
例8求y = arccos(sinx), ( )的值域
)的值域
解:設u = sin x ∵ ∴
∴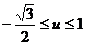
∴ ∴所求函數的值域為
∴所求函數的值域為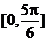
反正切函數

1°在整個定義域上無反函數
2°在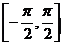 上
上 的反函數稱作反正切函數,
的反函數稱作反正切函數,
記作 (奇函數)
(奇函數)
2.已知三角函數求角:
求角的多值性法則:1、先決定角的象限 2、如果函數值是正值,則先求出對應的銳角x; 如果函數值是負值,則先求出與其絕對值對應的銳角x,3、由誘導公式,求出符合條件的其它象限的角
2、如果函數值是正值,則先求出對應的銳角x; 如果函數值是負值,則先求出與其絕對值對應的銳角x,3、由誘導公式,求出符合條件的其它象限的角
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com