
 ,M是弧AB的中點,OC⊥OD,△COD繞點O旋轉與△AMB的兩邊分別交于E、F(點E、F與點A、B、M均不重合),與⊙O分別交于P、Q兩點.
,M是弧AB的中點,OC⊥OD,△COD繞點O旋轉與△AMB的兩邊分別交于E、F(點E、F與點A、B、M均不重合),與⊙O分別交于P、Q兩點.
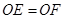 ;
;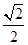 AB=6,再利用等角的余角相等得∠BOE=∠MOF,則可根據“SAS”判斷△OBE≌△OMF,所以OE=OF;
AB=6,再利用等角的余角相等得∠BOE=∠MOF,則可根據“SAS”判斷△OBE≌△OMF,所以OE=OF;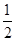 ∠BOQ,∠AMP=
∠BOQ,∠AMP=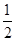 ∠AOP,則∠BMQ+∠AMP=
∠AOP,則∠BMQ+∠AMP=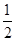 (∠BOQ+∠AOP)=45°,所以∠PMQ=∠BMQ+∠AMB+∠AMP=135°;
(∠BOQ+∠AOP)=45°,所以∠PMQ=∠BMQ+∠AMB+∠AMP=135°;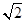 OE,再由△OBE≌△OMF得BE=MF,所以△EFM的周長=EF+MF+ME=EF+MB=
OE,再由△OBE≌△OMF得BE=MF,所以△EFM的周長=EF+MF+ME=EF+MB=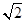 OE+6,根據垂線段最短得當OE⊥BM時,OE最小,此時OE=
OE+6,根據垂線段最短得當OE⊥BM時,OE最小,此時OE=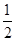 BM=3,所以△EFM的周長的最小值為9.
BM=3,所以△EFM的周長的最小值為9.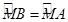 ,
,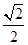 AB=
AB=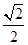 ×6
×6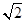 =6,
=6,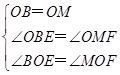 ,
,
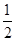 ∠BOQ,∠AMP=
∠BOQ,∠AMP=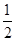 ∠AOP,
∠AOP,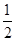 (∠BOQ+∠AOP),
(∠BOQ+∠AOP),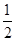 ×90°=45°,
×90°=45°,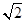 OE,
OE,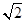 OE+6,
OE+6,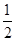 BM=
BM=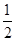 ×6=3,
×6=3,

科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
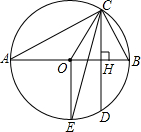
 的中點,連接0E,CE.求證:CE平分∠OCD.
的中點,連接0E,CE.求證:CE平分∠OCD.查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com