
2006年山東省濱州市中等學校招生統一考試
第Ⅰ卷(選擇題 共30分)
一、選擇題:本大題共10小題,每小題3分,共30分.在每小題給出的四個選項中,只有一項是符合題目要求的.請把選出的答案字母標號填在第Ⅱ卷前的答題表內,否則不得分.
1.函數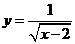 的自變量
的自變量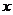 的取值范圍是( )
的取值范圍是( )
A.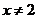 B.
B.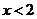 C.
C.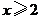 D.
D.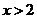
2.下列運算中,正確的是( )
A.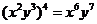 B.
B.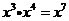
C.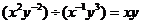 D.
D.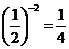
3.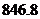 億度,用科學記數法記作(保留三位有效數字)( )
億度,用科學記數法記作(保留三位有效數字)( )
A.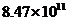 度 B.
度 B.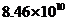 度 C.
度 C.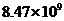 度 D.
度 D.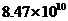 度
度
 4.如圖1,在半徑為10的
4.如圖1,在半徑為10的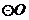 中,如果弦心距
中,如果弦心距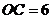 ,
,
那么弦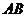 的長等于( )
的長等于( )
A.4 B.8
C.16 D.32
5.不等式組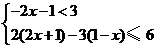 的解集為( )
的解集為( )
A.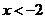 B.
B.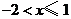 C.
C.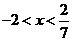 D.
D.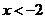 或
或
6.為建設生態濱州,我市某中學在植樹節那天,組織初三年級八個班的學生到西城新區植樹,各班植樹情況如下表:
班級
一
二
三
四
五
六
七
八
合計
棵數
15
18
22
25
29
14
18
19
160
下列說法錯誤的是( )
A.這組數據的眾數是18
B.這組數據的中位數是18.5
C.這組數據的平均數是20
 D.以平均數20(棵)為標準評價這次植樹活動中各班植樹任務完成情況比較合理
D.以平均數20(棵)為標準評價這次植樹活動中各班植樹任務完成情況比較合理
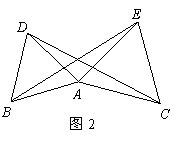
7.如圖2,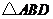 與
與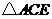 均為正三角形,且
均為正三角形,且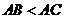 ,
,
則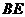 與
與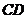 之間的大小關系是( )
之間的大小關系是( )
A.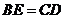 B.
B.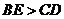
C.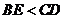 D.大小關系不確定
D.大小關系不確定
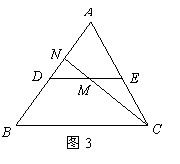 8.如圖3,
8.如圖3,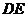 是
是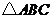 的中位線,
的中位線,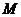 是
是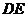 的中點,
的中點,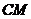 的
的
延長線交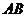 于點
于點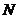 ,則
,則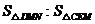 等于( )
等于( )
A.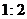 B.
B.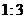
C.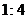 D.
D.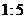
9.已知: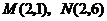 兩點,反比例函數
兩點,反比例函數 與線段
與線段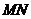 相交,過反比例函數
相交,過反比例函數 上任意一點
上任意一點 作
作 軸的垂線
軸的垂線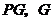 為垂足,
為垂足, 為坐標原點,則
為坐標原點,則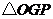 面積
面積 的取值范圍是( )
的取值范圍是( )
 A.
A.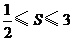 B.
B.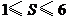 C.
C.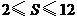 D.
D.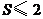 或
或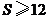
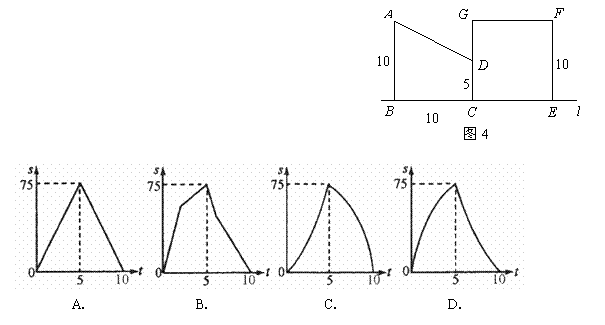
10.如圖4(單位:m),直角梯形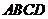 以
以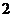 m/s的速度沿
m/s的速度沿
直線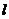 向正方形
向正方形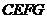 方向移動,直到
方向移動,直到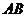 與
與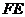 重合,直角
重合,直角
梯形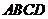 與正方形
與正方形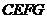 重疊部分的面積
重疊部分的面積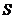 關于移動時間
關于移動時間
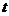 的函數圖象可能是( )
的函數圖象可能是( )
 第Ⅱ卷(非選擇題 共30分)
第Ⅱ卷(非選擇題 共30分)
二、填空題:本大題共8小題,每小題4分,共32分.把答案填在題中橫線上.
11.分式方程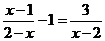 的解為
.
的解為
.
12.如圖5,在距旗桿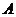 處,用測角儀測得旗桿頂端
處,用測角儀測得旗桿頂端
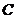 的仰角為
的仰角為 ,已知測角儀
,已知測角儀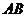 的高為
的高為
的高等于 米.
13.某同學對本地區2006年5月份連續六天的最高氣溫做了記錄,每天最高氣溫與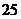 ℃的上下波動數據分別為
℃的上下波動數據分別為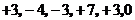 ,則這六天中氣溫波動數據的方差為 .
,則這六天中氣溫波動數據的方差為 .
 14.如圖6,已知等腰梯形
14.如圖6,已知等腰梯形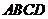 的周長是
的周長是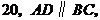
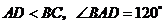 ,對角線
,對角線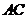 平分
平分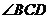 ,
,
則
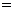 .
.
15.已知拋物線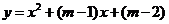 與
與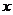 軸相交于
軸相交于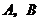 兩點,且線段
兩點,且線段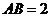 ,則
,則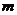 的值為
.
的值為
.
 16.已知二次函數不經過第一象限,且與
16.已知二次函數不經過第一象限,且與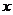 軸相交于不同的兩點,請寫出一個滿足上述條件的二次函數解析式 .
軸相交于不同的兩點,請寫出一個滿足上述條件的二次函數解析式 .
17.如圖7,在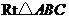 中,
中,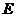 為斜邊
為斜邊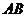 上一點,
上一點,
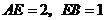 ,四邊形
,四邊形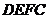 為正方形,則陰影
為正方形,則陰影
部分的面積為 .
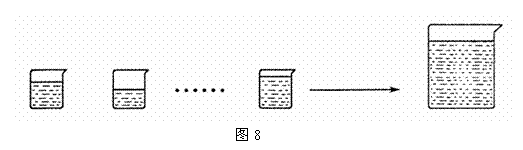
18.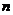 個小杯中依次盛有
個小杯中依次盛有 克糖水,并且分別含糖
克糖水,并且分別含糖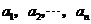 克.
克.
若這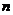 杯糖水的濃度相同,則有連等式
杯糖水的濃度相同,則有連等式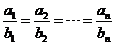 .
.
現將這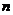 杯糖水合到一個大空杯中,則合杯糖水的濃度與各小杯糖水的濃度還是一樣的.
杯糖水合到一個大空杯中,則合杯糖水的濃度與各小杯糖水的濃度還是一樣的.
這個盡人皆知的事實,說明一個數學定理 等比定理:
等比定理:
若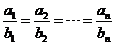 ,則
,則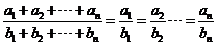 .
.
若這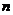 杯糖水的濃度互不相同,不妨設
杯糖水的濃度互不相同,不妨設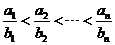 ,
,
現將這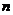 杯糖水合到一個大空杯中,則合杯糖水的濃度一定大于
,且小于 .
杯糖水合到一個大空杯中,則合杯糖水的濃度一定大于
,且小于 .
這個盡人皆知的事實,又說明了一個數學定理 不等比定理:
不等比定理:
 若
若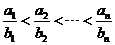 ,則
.
,則
.
三、解答題:本大題共7小題,共58分.解答應寫出文字說明、證明過程或演算步驟.
19.(本小題滿分5分)
解方程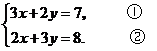
20.(本小題滿分7分)
已知 ,且
,且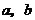 均為正數,先化簡下面的代數式,再求值:
均為正數,先化簡下面的代數式,再求值: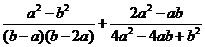 .
.
21.(本小題滿分8分)
如圖9,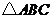 是一塊銳角三角形余料,邊
是一塊銳角三角形余料,邊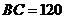 mm,高
mm,高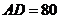 mm,要把它加工成長方形零件
mm,要把它加工成長方形零件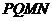 ,使長方形
,使長方形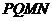 的邊
的邊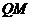 在
在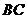 上,其余兩個頂點
上,其余兩個頂點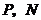 分別在
分別在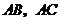 上.
上.
(Ⅰ)求這個長方形零件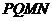 面積
面積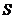 的最大值;
的最大值;
 (Ⅱ)在這個長方形零件
(Ⅱ)在這個長方形零件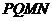 面積最大時,能否將余下的材料
面積最大時,能否將余下的材料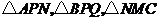 剪下再拼成(不計接縫用料及損耗)與長方形
剪下再拼成(不計接縫用料及損耗)與長方形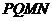 大小一樣的長方形?若能,試給出一種拼法;若不能,試說明理由.
大小一樣的長方形?若能,試給出一種拼法;若不能,試說明理由.
22.(本小題滿分8分)
假設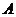 型進口汽車(以下簡稱
型進口汽車(以下簡稱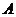 型車)關稅率在2001年是100%,在2006年是25%,2001年
型車)關稅率在2001年是100%,在2006年是25%,2001年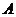 型車每輛的價格為64萬元(其中含32萬元的關稅).
型車每輛的價格為64萬元(其中含32萬元的關稅).
(Ⅰ)已知與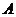 型車性能相近的
型車性能相近的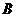 型國產汽車(以下簡稱
型國產汽車(以下簡稱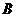 型車),2001年每輛的價格為46萬元,若
型車),2001年每輛的價格為46萬元,若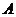 型車的價格只受關稅降低的影響,為了保證2006年
型車的價格只受關稅降低的影響,為了保證2006年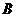 型車的價格為
型車的價格為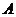 型車價格的90%,
型車價格的90%,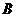 型車價格要逐年降低,求平均每年下降多少萬元;
型車價格要逐年降低,求平均每年下降多少萬元;
(Ⅱ)某人在2004年投資30萬元,計劃到2006年用這筆投資及投資回報買一輛按(Ⅰ)中所述降低價格后的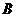 型車,假設每年的投資回報率相同,第一年的回報計入第二年的投資,試求每年的最低回報率.(參考數據:
型車,假設每年的投資回報率相同,第一年的回報計入第二年的投資,試求每年的最低回報率.(參考數據: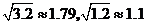 )
)
23.(本小題滿分8分)
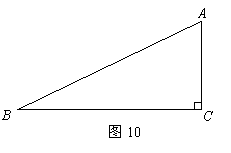
如圖10,已知直角三角形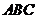 ,
,
(Ⅰ)試作出經過點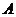 ,圓心
,圓心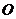 在斜邊
在斜邊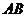 上,且與邊
上,且與邊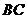 相切于點
相切于點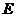 的
的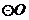 及切點
及切點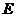 和圓心
和圓心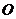 (要求:用尺規作圖,保留作圖痕跡,不寫作法和證明);
(要求:用尺規作圖,保留作圖痕跡,不寫作法和證明);
(Ⅱ)設(Ⅰ)中所作的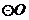 與邊
與邊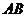 交于異于點
交于異于點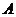 的另一點
的另一點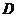 .求證:
.求證:
 (1)
(1)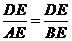 ;
;
(2)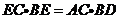 .
.
 24(本小題滿分10分)
24(本小題滿分10分)
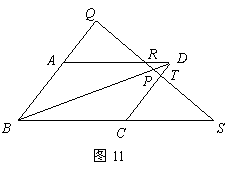
(Ⅰ)如圖11,點 在
在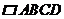 的對角線
的對角線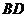 上,一直線過點
上,一直線過點 分別交
分別交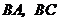 的延長線于點
的延長線于點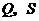 ,交
,交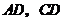 于點
于點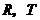 .
.
求證: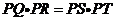 ;
;
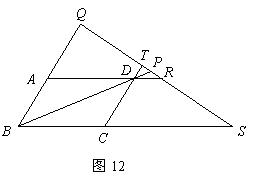 (Ⅱ)如圖12,圖13,當點
(Ⅱ)如圖12,圖13,當點 在
在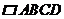 的對角線
的對角線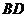 或
或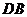 的延長線上時,
的延長線上時,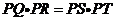 是否仍然成立?若成立,試給出證明;若不成立,試說明理由(要求僅以圖12為例進行證明或說明);
是否仍然成立?若成立,試給出證明;若不成立,試說明理由(要求僅以圖12為例進行證明或說明);
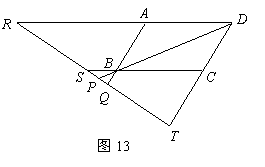
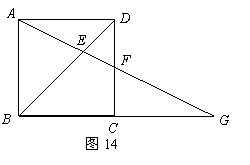 (Ⅲ)如圖14,
(Ⅲ)如圖14,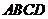 為正方形,
為正方形,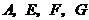 四點在同一條直線上,并且
四點在同一條直線上,并且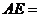
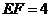 cm,試以(Ⅰ)所得結論為依據,求線段
cm,試以(Ⅰ)所得結論為依據,求線段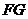 的長度.
的長度.
25.(本小題滿分12分)
已知:拋物線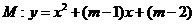 與
與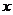 軸相交于
軸相交于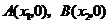 兩點,且
兩點,且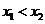 .
.
(Ⅰ)若 ,且
,且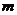 為正整數,求拋物線
為正整數,求拋物線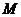 的解析式;
的解析式;
(Ⅱ)若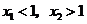 ,求
,求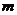 的取值范圍;
的取值范圍;
(Ⅲ)試判斷是否存在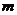 ,使經過點
,使經過點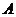 和點
和點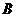 的圓與
的圓與 軸相切于點
軸相切于點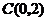 ,若存在,求出
,若存在,求出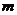 的值;若不存在,試說明理由;
的值;若不存在,試說明理由;
(Ⅳ)若直線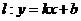 過點
過點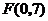 ,與(Ⅰ)中的拋物線
,與(Ⅰ)中的拋物線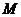 相交于
相交于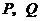 兩點,且使
兩點,且使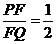 ,求直線
,求直線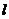 的解析式.
的解析式.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com