【題目】如圖，在四棱錐
中，平面
平面
，底面是邊長為2的正方形，且
，
.
（Ⅰ）證明：
；
（Ⅱ）求平面
與平面
所成二面角的正弦值.
習(xí)題精選系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】
年
月
日“世界讀書日”來臨之際，某校為了了解中學(xué)生課外閱讀情況，隨機抽取了
名學(xué)生，并獲得了他們一周課外閱讀時間（單位：小時）的數(shù)據(jù)，整理得到數(shù)據(jù)分組及頻數(shù)分布表.
組號 | 分組 | 頻數(shù) | 頻率 |
1 | [0，5） | 5 | 0.05 |
2 | [5，10） | a | 0.35 |
3 | [10，15） | 30 | b |
4 | [15，20） | 20 | 0.20 |
5 | [20，25] | 10 | 0.10 |
合計 | 100 | 1 | |
（1）求
、
的值
（2）作出這些數(shù)據(jù)的頻率分布直方圖
（3）假設(shè)每組數(shù)據(jù)組間是平均分布的，試估計該組數(shù)據(jù)的平均數(shù)和中位數(shù).（同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）若
在定義域上不單調(diào)，求
的取值范圍；
（2）設(shè)
分別是的極大值和極小值，且
，求
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某工廠生產(chǎn)的某產(chǎn)品按照每箱10件包裝，每箱產(chǎn)品在流入市場之前都要檢驗.若整箱產(chǎn)品檢驗不通過，除去檢驗費用外，每箱還要損失100元.檢驗方案如下：
第一步，一次性隨機抽取2件，若都合格則整箱產(chǎn)品檢驗通過；若都不合格則整箱產(chǎn)品檢驗不通過，檢驗結(jié)束，剩下的產(chǎn)品不再檢驗.若抽取的2件產(chǎn)品有且僅有1件合格，則進行第二步工作.
第二步，從剩下的8件產(chǎn)品中再隨機抽取1件，若不合格，則整箱產(chǎn)品檢驗不通過，檢驗結(jié)束，剩下的產(chǎn)品不再檢驗.若合格，則進行第三步工作.
第三步，從剩下的7件產(chǎn)品中隨機抽取1件，若不合格，則整箱產(chǎn)品檢驗不通過，若合格，則整箱產(chǎn)品檢驗通過，檢驗結(jié)束，剩下的產(chǎn)品都不再檢驗.
假設(shè)某箱該產(chǎn)品中有8件合格品，2件次品.
（Ⅰ）求該箱產(chǎn)品被檢驗通過的概率；
（Ⅱ）若每件產(chǎn)品的檢驗費用為10元，設(shè)該箱產(chǎn)品的檢驗費用和檢驗不通過的損失費用之和為
，求的分布列和數(shù)學(xué)期望
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知橢圓
的左頂點為
，過右焦點
的直線交橢圓于
，
兩點，直線
，
分別交直線
于點
，
.
（1）試判斷以線段
為直徑的圓是否過點，并說明理由；
（2）記
，
，
的斜率分別為
，
，
，證明：，，成等差數(shù)列.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，平行四邊形
所在平面與直角梯形
所在平面互相垂直，且
，
為
中點．
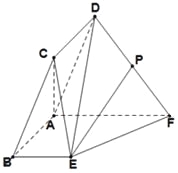
（1）求異面直線
與
所成的角；
（2）求平面
與平面所成的二面角（銳角）的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知四棱柱
的底面是邊長為
的菱形，且
，
平面
，
，
于點
，點
是
的中點.
（1）求證：
平面
；
（2）求平面
和平面所成銳二面角的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
