不等式的概念和性質
〖考綱要求〗掌握不等式的性質及其證明，能正確使用這些概念解決一些簡單問題.
〖復習建議〗不等式的性質是解、證不等式的基礎，對于這些性質，關鍵是正確理解和熟練運用，要弄清每一個條件和結論，學會對不等式進行條件的放寬和加強。
〖雙基回顧〗常見的性質有8條：
1、反身性（也叫對稱性）：a＞b
b＜a 2、傳遞性：a＞b，b＞ca＞c
3、平移性：a＞ba+c＞b+c
4、伸縮性：
ac＞bc；
ac＜bc
5、乘方性：a＞b≥0an＞bn（n∈N，n≥2）6、開方性：a＞b≥0
＞
（n∈N，n≥2）
7、疊加性：a＞b，c＞da+c＞b+d 8、疊乘性：a＞b≥0，c＞d≥0a?c＞b?d
一、知識點訓練：
1、下列結論對否：
（ ）
（ ）
（ ）
（ ）
（ ）
（ ）
2、
成立的充要條件為
3、用“＞”“＜”“＝”填空：
(1)a<b<c<0則ac bc ；
；
；
(2) 0<a<b<c<1，則ac bc ；ab ac；logca logcb；algc blgc；arcsina arcsinb.
二、典型例題分析：
1、比較下面各小題中a與b的大小：
(1)a=m3－m2n－3mn2 與 b=2m2n－6mn2＋n3 (2)a=3x2－x＋1與b=2x2＋x－1
(3)
.
2、a＞0，a≠1，t＞0，比較m=
與n=
的大小.
3、
，1≤
≤2，13≤
≤20，求
的取值范圍.
三、課堂練習：
1、若
，則下列不等式成立的是…………………………………………………………………
（ ）
(A)
(B)
(C) 
(D)
2、設
，那么下列不等式成立的是………………………………………………………
（ ）
(A)
(B)
(C)
(D)
以上都不對
3、已知
，則下列不等式能成立的是 …………………………………………………………（ ）
(A)
(B)
(C) (D) 
4、已知
，則下列不等式成立的是 ……………………………………………………（ ）
(A)
(B) 
(C)
(D)
5、若，則下列不等關系中不能成立的是
…………………………………………………… ( )
(A) 
(B)
(C)
(D)
四、課堂小結：
1、不等式的基本性質是解不等式與證明不等式的理論依據，必須透徹理解，特別要注意同向不等式可相加，也可相乘，但相乘時，兩個不等式都需大于零.
2、處理分式不等式時不要隨便將不等式兩邊乘以含有字母的分式，如果需要去分母，一定要考慮所乘的代數式的正負.
3、作差法是證明不等式的最基本也是很重要的方法，應引起高度注意.
五、能力測試： 姓名 得分
1、下列命題中正確的是……………………………………………………………………………… ( )
(A)
(B) 
(C) 
(D)
2、設
，則有 …………………………………………………………………………………（ ）
(A) (B)
(C) 
(D)
3、若
,則有…………………………………………………………………… ( )
(A) 
(B)
(C)
(D)以上皆錯
4、若
,則 ………………………………………………………………………………( )
(A) 
(B)
(C)
(D)c、d大小不確定
5、以下命題：⑴a>b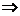
|a|>b ⑵a>b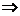a2>b2 ⑶|a|>b 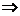a>b ⑷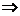a>|b| a>b
正確的個數有………………………………………………………………………………………（ ）
(A) 1個 (B) 2個 (C) 3個 (D)4個
6、已知a＞
,比較
與的大小.
7、比較下列各數的大小：
(1)
（提示：分a＞1，a＜1討論）
(2)
與
（提示：分子有理化后再比較）
8、如果二次函數
的圖象過原點，并且1≤
≤2,3≤≤4,求
的取值范圍.
不等式的解法――分式與高次
〖考綱要求〗在熟練掌握一元一次與一元二次不等式的解法的基礎上初步分式與高次不等式的解法.
〖復習建議〗分式與高次不等式的一般解法：序軸標根法，能注意到其中的一些特殊點與解集的關系，能注意到區間端點與解集的關系.
一、知識點訓練：
1、下列不等式與
同解的是……………………………………………………………（ ）
(A) 
(B)
(C)
(D)
2、不等式(x－2)2?(x－1)>0的解集為 .
3、不等式(x＋1) ?(x－1)2≤0的解集為 .
4、不等式
的解集為
.
二、典型例題分析：
1、解不等式：(x－1)?(x－2)?(x－3)?(x－4)>120
2、解不等式：
3、解不等式：
4、若不等式
對一切x恒成立,求實數m的范圍
5、求適合不等式
的整數x的值.
6、解關于x的不等式
三、課堂練習：
1、不等式
的解集為……………………………………………………………………（ ）
(A){x|
≤x≤2}
(B) {x|≤x<2}
(C) {x|x>2或者x≤} (D){x|x＜2
2、不等式
的解集為
.
3、如果不等式
的解集為（
，1），則
=
.
分式與高次不等式的解題基礎是一元二次不等式的解法，常用方法是序軸標根法，但是要注意標根時的起點位置.
五、能力測試：
四、課堂小結：
1、與不等式
同解的不等式是……………………………………………………………（ ）
(A)(x－3)(2－x)≥0 (B)lg(x－2)≤0 (C) 
(D)(x－3)(2－x)>0
2、如果x1<x2<…<xn，n≥2,并且{x|(x－x1)(x－x2)…(x－xn)>0}
{x|x2－(x1＋x2)x＋x1x2<0}，那么自然數n…………………………………………………………………………………………………（ ）
(A)等于2 (B)是大于2的奇數
(C) 是大于2的偶數 (D)是大于1的任意自然數
3、不等式(x－1)(x＋2)(3－x)>0的解集為 .
4、不等式
的解集為
.
5、a>0,b>0，那么不等式
的解集為
.
6、已知不等式
的解集為{x|x<1或x>2}，那么a=
.
7、解不等式：
（提示：
）
8、不等式
對一切x都成立，求n的值.
9、解關于x的不等式
不等式的解法――指數 對數（無理不等式）
〖考綱要求〗新的考綱雖然沒有明確要求掌握簡單的指數、對數無理不等式的解法，但是卻要求掌握函數的單調性，會利用函數單調性比較大小，而這也正是我們這一講的出發點..
〖復習建議〗1、掌握解指數、對數不等式的方法，一般來說，與解指數、對數方程的方法類似.即：
(1)同底法：能化為同底數先化為同底，再根據指數、對數的單調性轉化為代數不等式，底是參數時要注意對其進行討論.并注意到對數真數大于零的限制條件.
(2)轉化法：多用于指數不等式，通過兩邊取對數轉化為對數不等式（注意轉化的等價性）.
(3)換元法：多用于不等式兩邊是和的形式，或取對數后再換元，并注意所換“元”的范圍.
2、掌握基本無理不等式的轉化方法.
一、知識點訓練：
1、當
等價的不等式是 …………………………………（ ）
（A）
（B）
（C）
（D）以上都不對
2、當
等價的不等式是 …………………………………………………（ ）
（A）
（B）（C）
（D）
3、不等式
的解集為……………………………………………………………（ ）
（A）{x|x<2} （B）{x|0<x<2} （C）{x|1<x<2} （D）{x|x>2}
4、不等式(x－1)
的解為……………………………………………………………（ ）
(A)x≥1 (B)x>1 (C) x≥1或者x=－2 (D) x≥－2且x≠1
5、不等式
的解集為
；
二、典型例題分析：
1、解不等式
2、解不等式
.
3、如果x=3是不等式：
的一個解，解此關于x的不等式.
4、解關于x的不等式：
*5、解不等式：
三、課堂練習：
1、不等式
的解集為 ；
2、不等式
的解集為 ；
3、不等式
的解集是 ……………………………………………………………（ ）
（A）
（B）
（C）
（D）
掌握指數、對數、無理不等式的常規解法―取對數法、換底法、換元法、利用函數單調性，將它們轉化為代數不等式.在進行轉化時，應充分注意函數定義域，保證同解變形.在轉化為求不等式組的解時，應注意區別“且”、“或”，涉及到最后幾個不等式的解集是“交”，還是“并”.
五、能力測試：
四、課堂小結：
1、與不等式
同解的不等式是 …………………………………………………………（ ）
（A）
（B）
（C）
（D）
2、不等式
的解為 ……………………………………………………………………（ ）
（A）x>11 （B）x<－9 （C）x<－9或x>11 （D）－9<x<11
3、設c<0，下列不等式成立的是 ……………………………………………………………………（ ）
（A）
（B）
（C）
（D）
4、不等式
的解集為……………………………………………………………………（ ）
（A）{x|x≤1} （B）{x|＜x≤1 （C）{x|＜x＜1 （D）R
5、不等式
的解集為 ……………………………………………………………………（ ）
（A）
（B）
(C)
（D）
6、
的同集不等式為 …………………………………………………（ ）
(A)
(B)
(C)
(D）
7、
8、不等式lgx＋lg(x－3)<1的解集為 .
9、解關于x的不等式：
*10、解不等式
不等式的證明―比較法
〖考綱要求〗掌握不等式的性質及其證明，能正確使用這些性質解決一些簡單問題.
〖復習建議〗掌握求差法與求商法比較兩個數的大小。
〖雙基回顧〗
1、求差法：a＞b
a－b＞0
2、求商法：a＞b＞0
3、用到的一些特殊結論：同向不等式可以相加（正數可以相乘）；異向不等式可以相減；
一、知識點訓練：
1、已知下列不等式:
其中正確的個數為 ……………………………………………………………………………………( )
(A)0 (B)1 (C) 2 (D) 3
2、1＞a＞b＞0，那么…………………………………………………………………………………（ ）
(A)a＞
＞
＞b
(B) b＞＞＞a
(C) a＞＞b＞
(D) ＞＞a＞b
3、如果－
＜b＜a＜，則b－a的取值范圍是……………………………………………………（ ）
(A)－
＜b－a＜0 (B) －
＜b－a＜ (C)
－＜b－a＜0 (D) －＜b－a＜
4、已知
1.（填“>”或者“<”）
二、典型例題分析：
1、求證：若a、b>0,n>1,
2、a、b、c、d、m、n全是正數，比較p=
q=
的大小.
3、比較
的大小
4、a∈R，函數
(1)判斷此函數的單調性。
(2)F(n)=
,當函數為奇函數時，比較
的大小.
三、課堂練習：
1、a＞b
與同時成立，那么有………………………………………………………………（ ）
(A) a＞b＞0
(B) a＞0＞b (C) ＞0
(D) 
2、
四、課堂小結：
比較法是證明不等式最常用最基本的方法.當欲證的不等式兩端是多項式或分式時，常用差值比較法。當欲證的不等式兩端是乘積的形式或冪指不等式時常用商值比較法，即欲證
五、能力測試： 姓名 得分
1、不等式：⑴x3＋3>2x；⑵a5＋b5<a3b2＋a2b3；⑶a2＋b2≥2(a＋b－1)；⑷
恒成立的有( )
(A)⑴、⑵ (B) ⑴、⑶ (C) ⑶、⑷ (D) ⑴、⑵、⑶、⑷
2、
對
都成立的不等式是…………………………………………………………………… ( )
(A)
(B) 
(C) 
(D)
3、0＜a＜1，F=
，G=
，H=
，那么F、G、H中最小的是…………………………（ ）
(A)F (B) G (C) H (D) 不能確定
4、a>b>0，則下列不等式恒成立的是………………………………………………………………（ ）
(A)
(B)
(C)
(D)
aa>bb
5、x>100，那么lg2x,lgx2,lglgx從大到小的順序為 .
6、a＞0，b＞0，a＋b=1，比較M=x2＋y2與N=(ax＋by)2＋(bx＋ay)2的大小.
7、比較
大小
8、求證：
9、比較A=a6＋a4＋a2＋1與B=a5＋a3＋a的大小.（提示：分a＞1，a=1，a＜1討論）
證明：a＞1時，A－B=a6＋a4＋a2＋1－（a5＋a3＋a）=(a6－a5)＋(a4－a3)＋(a2－a)＋1
不等式證明的其它方法
〖考綱要求〗掌握用“分析法”證明不等式；理解反證法、換元法、判別式法、放縮法證明不等式的步驟及應用范圍.
〖復習建議〗搞清分析法證題的理論依據，掌握分析法的證題格式和要求。搞清各種證明方法的理論依據和具體證明方法和步驟。
說明：數學歸納法法證明不等式將在數學歸納法中專門研究.
〖雙基回顧〗
1、“分析法”證題的理論依據：尋找結論成立的充分條件或者是充要條件.
2、“分析法”證題是一個非常好的方法，但是書寫不是太方便，所以我們可以利用分析法尋找證題的途徑，然后用“綜合法”進行表達.
一、知識點訓練：
1、推理：如果a≠b，要證a2＋b2<1＋a2b2，由于2ab<a2＋b2，只要證：2ab<a2＋b2 正確嗎？
2、推理：要證|a＋b|≤|a|＋|b|，只要證|a＋b|2≤(|a|＋|b|)2 正確嗎？
3、推理：要證a<b，只要證a2<b2 對嗎？
4、a、b、c∈R，a＞b是ac2＞bc2成立的…………………………………………………………（ ）
(A)充分條件 (B)必要條件 (C)充要條件 (D)既不充分又不必要條件
二、典型例題分析：
1、x＞0，y＞0，求證：
2、a＞b＞0，2c＞a＋b，求證：
3、函數
，求證：
4、
（三角換元法）
5、求證：
（判別式法）
6、若a,b,c都是小于1的正數，求證：
（反證法）
7、求證：
（放縮法）
三、課堂練習：
1、a＞b＞0，求證：
2、A、B、C是ㄓABC的內角，求證：x2＋y2＋z2≥2yzcosA＋2zxcosB＋2xycosC.（判別式法）
四、課堂小結：
1、“分析法”證明不等式就是“執果索因”，從所證的不等式出發，不斷利用充分條件或者充要條件替換前面的不等式，直至找到顯然成立的不等式，書寫方法習慣上用“
”來表達.
2、凡是“至少”、“唯一”或含有否定詞的命題適宜用反證法.
3、換元法（主要指三角代換法）多用于條件不等式的證明，此法若運用恰當，可溝通三角與代數的聯系，將復雜的代數問題轉化成簡單的三角問題.
4、含有兩上字母的不等式，若可化成一邊為零，而另一邊是關于某字母的二次式時，這時可考慮判別式法，并注意根的取值范圍和題目的限制條件.
5、有些不等式若恰當地運用放縮法可以很快得證，放縮時要看準目標，做到有的放矢，注意放縮適度.
五、能力測試： 姓名 得分
1、如果P=
，Q=1+
，R=
，那么有………………………………………………（ ）
(A)P＞Q＞R (B)R＞P＞Q (C) Q＞R＞P (D)R＞Q＞P
2、a＞b＞0，那么下列不等式中恒成立的是………………………………………………………（ ）
(A)
(B) 
(C) 
(D)
3、四個命題：⑴a2＜b2|a|＜|b| ⑵ a2＜b2a＋b與a－b符號相反 ⑶a2＜b2|a|＋|b|與|a|－|b|符號相反 ⑷a2＜b2|a|2＜|b|2符號相反 其中是真命題的有……………………………（ ）
(A) 4個 (B)3個 (C) 2個 (D)1個
4、x、y∈R，|x|＜1，|y|＜1是0＜xy＜1的………………………………………………………（ ）
(A) 充分條件 (B)必要條件 (C) 充要條件 (D)既不充分也不必要條件
5、a、b、c∈R-，a≠b，求證：
6、a＞b＞c，求證：
（提示：換元法，令a－b=m∈R＋，b－c=n∈R＋）
7、求證：
8、證明不等式：
（提示：使用放縮法
）
9、x＞0，y＞0并且x+y＞2，求證
中至少有一個小于2（提示：反證法）
不等式的應用
〖考綱要求〗
1、熟練運用不等式的知識綜合解決函數、方程等中的有關問題.
2、在掌握一次函數單調性、二次函數的最值以及在定區間上的最值問題，學會變量的轉換，掌握：恒正、恒負、解集為R、解集為空集的實際含義并且會轉化
3、掌握 “兩個正數的算術平均數不小于他們的幾何平均數”，并能運用此定理解決一些問題.
〖復習建議〗重要不等式的功能在于和積互化，要注意三個條件：一正、二定、三相等的檢驗。在運用過程中，要注意創造特殊的環境：
一、知識點訓練：
1、下列函數中，最小值為4的是………………………………………………………………… ( )
(A)
(B)
(C) 
(D)
2.當x
時，等式
成立；
當x
時，等式
成立.
二、典型例題分析：
1、若
的最值.
2、
的最小值.
3、
時恒正，求x的取值范圍（關于a的一次函數）.
4、函數
=x2＋ax＋3，當x∈[－2，2]時，恒有≥a，求a的最小值.
5、已知函數，x∈[a，b]，如果對任意的x∈[a，b]，都有
，則就稱可以被函數y=
“替代”.試判斷：函數
，x∈[4，16]是否可以被函數=
，x∈[4，16]替代，并且說明理由！
*6、設函數是定義在R上的單調函數并且滿足：
，
⑴求證：為奇函數 ⑵為減函數
⑶如果
+
>0恒成立，求實數k的取值范圍.
三、課堂練習
1、
有意義，則實數a的取值范圍是
.
2、
，則實數a的取值范圍是
.
四、能力測試
1、若x+2y=4,且x>0,y>0,則 lgx+lgy的最大值為 ……………………………………………………（ ）
（A）2 （B）2lg2
（C）lg2
（D）
2、設a,b為實數，且a+b=3,則2a+2b的最小值是 ……………………………………………………（ ）
（A）6 （B）
（C）
（D）8
3、函數
圖象上最低點的坐標為………………………………………………（ ）
（A）（0，5）
(B) （3，4）
(C) （3，2）
(D) （8，
）
4、x、y∈R+，那么不等式
恒成立的最小正數a= .
5、(1)若
的最大值是 ；(2)函數tgx+ctgx的值域是 ；
6.現有含鹽7%的食鹽水200克，生產上需要含鹽在5%以上，6%以下的食鹽水，設需要加入含鹽
4%的食鹽水x克，則x的范圍是 .
7、函數y=x2＋ax＋3的圖象恒在函數y=2ax－5的上方，求實數a的取值范圍.
8、定義在
上的函數y=單調遞減，是否存在實數k，使：
對一切實數恒成立？存在請求出，不存在請說明理由！
*9、對滿足：|p|＜2的一切p，不等式
＋p
＋1＞2＋p恒成立，求實數x的取
值范圍（提示：可以理解為關于p的一次函數）.
不等式的應用2
〖考綱要求〗
能運用不等式的知識解決實際問題.
〖復習建議〗
能從實際問題中抽象出數學模型，尋找出該數學模型中已知量與未知量，建立數學關系式，并用適當的方法解決問題。
一、典型例題分析：
1、已知三角形的三邊長分別為15，19，23厘米，把它的三條邊長分別縮短x厘米，使它只能構成鈍角三角形，求x的取值范圍.
2、從邊長為2a的正方形鐵皮的四角各截去一小塊邊長為x的正方形，再將
四邊向上折起，做成一個無蓋的方鐵盒，問x取何值時，盒的容積最大？
最大的容積為多少？
3、某雜志若以每本2元的價格出售，可以發行10萬本，若每本價格提高0.2元，發行量就少5000
本，要使銷售總收入不低于22.4萬元，則該雜志的定價最高和最低各為多少？
4、在某種商品生產過程中，每日次品數y是每日產量x的函數：
，該產品每售出一件正品獲得利潤A元，每生產一件次品就損失
元，為了獲得最大利潤，日產量應該是多少？
5、（12分）在某海濱城市附近海面有一臺風，根據監測，當前臺風中心位于城市O（如圖）的東偏南
（
）方向300km的海面P處，并且以20km/h的速度向西偏北45°方向移動，臺風侵襲的范圍為圓形區域，當前半徑為60km，并且以10km/h的速度不斷增大，問幾個小時后，該城市開始受到臺風的侵襲？
*6、甲、乙兩地相距240千米,汽車從甲地勻速行駛到乙地,速度不得超過60千米/時.已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度v(千米/時)的平方成正比,比例系數為b；固定部分為a元.
⑴全程運輸成本把y(元)表示為速度v(千米/時)的函數,并指出這個函數的定義域;
⑵為了使全程運輸成本最小,汽車應以多大速度行駛?
二、研究題：
1、等邊圓錐母線長為8，其的內接圓柱的高為x，當內接圓柱側面積最大時，x的值為………（ ）
（A）3
（B）2
（C）
（D）4
次
案
第一次提價
第二次提價
甲
p%
q%
乙
q%
p%
丙
2、某商店計劃兩次提價，有甲、乙、丙三種方案，(如右表，其
中p>q>0.)經兩次提價后，則 種方案的提價幅度最大！
3、某工廠生產一種文具所需支付的費用有三種：
⑴不論生產不生產，都需支付職工工資等固定開支1.25萬元；
⑵生產x件產品，所需各種原材料費用，平均每件36元；
⑶由于能源供應的特殊政策，經測算，生產x件產品的能源
費為每件0.05x元.
問這種文具平均每件生產成本最低是多少元？
4、某工廠有舊墻一面14米，現在準備利用這面舊建造平面圖形為矩形、面積為126平方米的廠房，條件是⑴建1米新墻的費用為100元；⑵修1米舊墻的費用為25元；⑶拆1米舊墻，用所得的材料建1米新墻的費用為50元，現在有兩種方案：
第一種：利用舊墻的一面長為x米（0<x<14米）；
第二種：利用舊墻的一面長為x米（x≥14米）. 問：那一種方案好？最少費用是多少？
5、某輪船公司爭取到一個相距1000海里的甲、乙兩地的航運權，已知輪船限載400人，輪船每小時的燃料費用和輪船的速度的立方成正比，輪船的最大時速為25海里/小時，當航速為10海里/小時時，它的燃料費用為30元/小時，其余費用（與速度無關）都是480元/小時，如果公司打算從每個顧客身上獲得平均利潤a元，在輪船滿載航行時，你能為該公司設計一種比較合理的船票價格嗎？為什么！
*6、某保健中心用60萬元買進一臺儀器，該儀器第一年的保養、維修費為1.2萬元，以后每年保養、
維修費都比上一年增加2千元，第一年管理人員工資費用2萬元，以后每年比上一年增加5%，
據調查平均每年有1000人次使用次儀器，如果計劃10年收回投資（含購買、保養、維修、工資等），問每人檢查一次應該收費不少于多少元？
*7、設計一宣傳畫，要求畫面面積4840cm2，畫面的寬與高的比為
（<1）,畫面的上下各留8cm空白,左右各留5cm空白,怎樣確定畫面寬與高的尺寸,才能使宣傳畫所有的紙張面積最小?如果要求∈[
],那么為何值時, 才能使宣傳畫所有的紙張面積最小?(2001廣東題)
高三數學總復習測試――不等式
姓名 得分
一、選擇題
1、四個命題：⑴a>b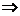|a|>b；⑵a>b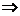a2>b2；⑶|a|>b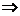a>b；⑷a>|b|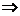a>b
正確的共有…（ ）
(A)1個 (B)2個 (C) 3個 (D)4個
2、如果1<a<b,a+b=1,那么四個數：b，2ab，，
最大的是…………………………（ ）
(A)b (B)2ab
(C)
(D)
3、1＞x＞0，下列三個數：a=
，b=1＋x，c=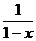
，則其中最大的一個是……………………（ ）
(A)a (B) b (C) c (D) 不能確定
4、不等式組
有解，則實數a的取值范圍是……………………………………………（ ）
(A)(－1,3) (B) (－3,1)
(C) (－∞,－1)∪(3,＋∞) (D) (－∞,－3)∪(1,＋∞)
5、x是實數，則下列不等式恒成立的是……………………………………………………………（ ）
(A) 
(B) (C)
(D) 
6、如果實數x、y、m、n滿足x2＋y2=a，m2＋n2=b，則mx＋ny的最大值為……………………（ ）
(A) (B) (C)
(D)
7、如果a，b＞0，并且4x+y=a，如果xy的最大值為16，那么常數a=………………………………（ ）
(A)8 (B) 64 (C) 32 (D) 16
8、下列函數中，最小值為2的是……………………………………………………………………（ ）
(A)
(B)
(C)
(D)
9、不等式
的解集為…………………………………………………………………（ ）
(A)(0,1) (B)(0,＋∞) (C) (1,＋∞) (D) (－∞，1)
10、如果
的值恒為正數，那么a的取值范圍是………………………………………（ ）
(A)a＞
(B)
(C)a＞1 (D)
a＞1或
11、如果不等式：|x－2|+|x－5|≥a的解集為R，那么實數a的取值范圍是………………………（ ）
(A)
(B) 
(C) 
(D) 
12、如果方程：x2－x－(m＋1)=0在[－1，1]上有解，則m的范圍是…………………………………（ ）
(A)
(B) 
(C) 
(D) 
二、填空題
13、不等式：(a2－1)x2－(a－1)x－1<0對任意實數都成立，那么實數a的取值范圍是 .
14、不等式組
的解集為 .
15、如果關于x的不等式：x2－ax－4<0的解集是(－1,m)，那么a= ；m= .
16、設a、b、x都是正數，且a、b是常數，則函數
的最小值為
.
三、解答題
17、解不等式：
18、一批貨物隨17列貨車從A地以vkm/h的速度勻速直達B地，已知兩地鐵路線長400km，為了安全，兩貨車距離不得小于
km，求這批貨物全部抵達B地所需要的最少時間！
19、已知奇函數在定義域（－1，1）上單調遞減，并且滿足：
，
求實數a的取值范圍.
20、某小區要建一個面積為a平方米的矩形綠地，四周有小路，綠地長邊外路寬5米，短邊外小路寬8米，綠地邊長至多長28米，最小長20米，對于給定的a（300≤a≤700），怎樣設計綠地的長與寬，使綠地和小路所占的總面積最小！
 |
21、已知曲線C1的方程為xy=－1，曲線C1關于點M（－，）的對稱曲線為C2.
⑴求曲線C2的表達式并求函數的單調區間；
⑵如果
，求證：
22、已知二次函數=ax2＋bx＋c（a、b、c是實數）同時滿足下列條件：⑴
；⑵對任意實數x，都有－x≥0；⑶當x∈（0，2）時，有
.
⑴求；
⑵求a、b、c；
⑶當x∈[－1，1]時，=－mx（m是實數）是單調函數，求實數m的取值范圍.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com